Marching Events: What does iCalendar have to do with ray marching?
Recently I've been cursed blessed with the opportunity of
implementing a library for operating on iCalendar files. If you
haven't heard of them, you probably have - it's the format used to
transfer e-mail RSVPs, to name a thing:
Despite iCal's age - RFC 2245 is dated 1998, same as the Clinton-Lewinsky scandal - I think it's a Pretty Good Format™. It's reasonably easy to print and parse:
BEGIN:VEVENT UID:1234-1234-1234-1234 DTSTAMP:20250608T160000Z DTSTART:20250628T160000Z DTEND:20250628T190000Z SUMMARY:Found some good candles in my neighbour's trash, gonna snort 'em. CATEGORIES:BUSINESS END:VEVENT
... and supports a ton of things - today the limelight shines on recurring events.
- > It's a Date!
- > Computer Liebe
- > The Math of Love Triangles
- > Marching events
- > Atoms
- > Yield Me Maybe
- > Molecules
- > Closing thoughts
It's a Date!
I'm a simple boy - to me recurring means a simple thing like "every day" or "every week"; world ain't no simple place, though.
How do we tame this? iCalendar proposes we define:
-
FREQ, saying how an event repeats (hourly, daily, weekly, ...), DTSTART, saying from when an event repeats,
... and that's basically it, at least when it comes to required properties:
-> 2018-01-01 12:00:00 -> 2018-01-01 13:00:00 -> 2018-01-01 14:00:00 -> [...]
We can also specify INTERVAL, which produces multiplies
of the frequency:
-> 2018-01-01 12:00:00 -> 2018-01-04 12:00:00 -> 2018-01-07 12:00:00 -> [...]
But that's boring, that's something you could've come up with on your own - here's something fun:
starting from 2018-01, repeat every other month on its first and last day, but only if that day is Monday: -> 2018-01-01 -> 2019-07-01 -> 2019-09-30 -> 2020-11-30
... and here's something pragmatic:
starting from 2018-01, repeat every month on its last workday: -> 2018-01-31 (Wednesday) -> 2018-02-28 (Wednesday) -> 2018-03-30 (Friday) -> [...]
You might see where this is going:
given an iCal formula, how do we figure out when it repeats?
Computer Liebe
Sounds easy, right? Or maybe not easy-easy, but - like - doable.
Even if you're aware of potential roadblocks (how's repeating defined across time zone transitions?), you might have this thought that intuitively this shouldn't be a terribly difficult thing to implement.
And you'd be right, somewhat.
Most implementations tend to have some sort of hand-unrolled, frequency-specific logic:
fn iter(recur: &Recur) -> impl Iterator<Item = DateTime> { match recur.freq { "yearly" => iter_yearly(recur), "monthly" => iter_monthly(recur), "daily" => iter_daily(recur), /* ... */ } } /* ... */ fn iter_monthly(recur: &Recur) -> impl Iterator<Item = DateTime> { let mut curr = recur.dtstart; loop { if recur.by_month_day.is_empty() { // FREQ=MONTHLY;INTERVAL=3 simply repeats the DTSTART with // consecutive freq-based increments yield curr; } else { // FREQ=MONTHLY;BYMONTHDAY=10,20,30 creates *new* dates that are // based on the currently iterated-over date for day in recur.by_month_day { yield curr.with_day(day); } } curr += Span::Year * recur.interval; } } /* ... */
That's because depending on context, a parameter can function either as a filter:
for day in days_since(dtstart) { if day.is(Monday) { yield day; } }
... or as a generator:
for month in months_since(dtstart) { for day in month.every(Monday) { yield day; } }
RFC collects all of those cases into a rather spooky-looking table:
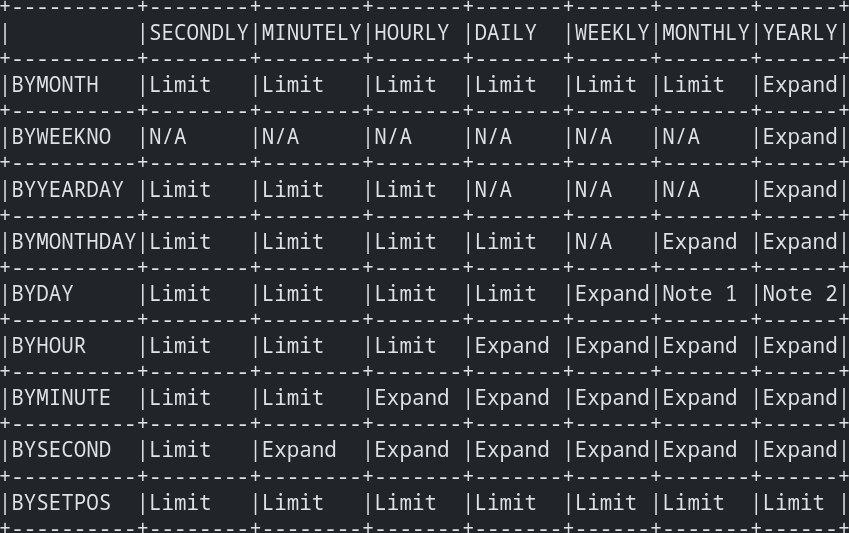
... whose apparent complexity is what causes libraries to implement iCal features just partially, like with libical and the BYSETPOS rule - since it must be provided for each context in which it appears, it's naturally implemented only for the common use cases.
(not a nitpick towards libical, it's just an example i'm aware of.)
That's the way I started my implementation as well, but something about it felt off to me - I had a feeling there must be a better way to approach this.
I began to imagine those recurrence rules as SQL queries:
select day from dates -- infinite table of all possible dates where day_of_week(day) = 'Monday' and day >= '2018-01-01'
select day from dates where day_of_week(day) = 'Monday' or day_of_week(day) = 'Tuesday' and day_of_month(day) = 10 and day >= '2018-01-01'
... and then I realized that under this framework, the
FREQ rule disappears - FREQ=DAILY;BYDAY=MO,
FREQ=WEEKLY;BYDAY=MO and
FREQ=MONTHLY;BYDAY=MO all correspond to the same query,
even though in one case BYDAY
functions as a filter, while in the others it's a generator:
select day from dates where day_of_week(day) = 'Monday' and day >= '2018-01-01'
Having this, I started to think about how I would materialize this
query - naively we could just iterate through all of the possible
dates and check whether all conditions match (modulo the
>= '2018-01-01' part, since this hypothetical
dates table is infinite). But maybe there's a better way?
And then I realized there's a thing I can steal borrow from the
rendering community.
The Math of Love Triangles
Triangles are those pointy, pointy, sexy bois:
... whose life purpose is illustrating Pytagorean
Pythagoran Pytagoream Pythagorean theorem - they also
tend to be used for modelling stuff in computer graphics and
whathaveyou:
Triangles are cool, because GPUs can draw millions of them per second, but simplicity in rendering comes at a cost. Certain operations - like figuring out the difference of two shapes:
... are rather awkward when operating on triangles (aka polygons).
Another way of thinking about shapes is by describing them analytically, with the most popular approach (citation needed) being via signed distance functions.
A signed distance function accepts a point and returns a distance from that point towards the nearest surface. You might think it sounds like a difficult kind of thing to implement, but it's actually quite straightforward - for instance the SDF of a sphere of radius=1 centered at xyz=(0,0,0) is just:
struct Vec3 { x: f32, y: f32, z: f32, } fn sphere(point: Vec3) -> f32 { // Calculate distance from origin (0,0,0) to given point let dist_to_origin = ( point.x * point.x + point.y * point.y + point.z * point.z ).sqrt(); dist_to_origin - 1.0 }
... because:
sphere(vec3(2.0, 2.0, 2.0)) =~ 2.46 // ^ we're 2.46 units away from the nearest sphere sphere(vec3(0.57, 0.57, 0.57)) =~ 0.0 // ^ we're exactly *at* the sphere (0.57 = 1/sqrt(3)) sphere(vec3(0.0, 0.0, 0.0)) = -1.0 // ^ we're -1.0 units past the surface of sphere (we're inside of the shape)
Notably, an SDF returns zero when given point is located directly on the surface represented by the function - so if we wanted to render this surface, we'd take a camera:
... and a viewport (a canvas onto which we're projecting the image):
... and then for each pixel of this viewport we'd shoot a ray from the camera, through the viewport, outward towards the world:
... and we'd slowly march through each of those rays, looking for places where SDF returns zero, indicating that the particular ray has reached a surface:
fn render_image( sdf: fn(Vec3) -> f32, camera: Camera, ) -> Image { let mut image = Image::new(width, height); for x in 0..width { for y in 0..height { let mut curr = camera.origin; let dir = camera.ray((x, y)); for _iter in 0..128 { if sdf(curr) == 0.0 { // Yay, reached the surface! image.set_color(x, y, Color::Green); break; } // Nay, not yet - make a small step forward! curr += 0.01 * dir; } } } image }
Marching in constant steps is inefficient, though - it doesn't make a
good use of the SDF, because it treats it as a binary function (0 => yay, != 0 => nay), while in reality the SDF tells us much
more.
Instead of taking constant-length steps, we can use the value returned from the SDF as a guide of how long step we can make - this is known as sphere tracing:
for _iter in 0..128 { let step = sdf(point); if step == 0.0 { image.set_color(x, y, Color::White); break; } curr += step * dir; }
You might think:
but since the function tells us where the closest surface is, can't we do it in
O(1)by simply calling the function once, why the loop ??
Unfortunately, we have to call the SDF multiple times, because this function only tells us about the distance to the closest surface, not about distance to the closest surface that coincides with the direction we're walking towards:
So the specific property is that an SDF returns zero when we're at the surface and otherwise it returns a distance to the nearest surface, or at most an underapproximation of this distance.
Marching events
Cool, but what all of that has to do with recurring events?
I've found a way of describing occurrences through distance functions. This means that instead of implementing logic for all combinations of frequencies and parameters - as that spooky table from before suggests one might do - we can simply compose a couple of distance functions together.
Instead of 7 (frequencies) * 9 (BY* parameters) code
paths, we end up with 7 + 9.
Similarly to SDFs, what we're looking for is a function that takes a date, returns a span (+1 hour, +2 days etc.), and satisfies the following properties:
-
if
dateis an occurrence of the event, this function returns zero, - otherwise this function returns a positive span that either points at the next occurrence or it's an underapproximation of it.
Having those as the only requirements means we're given a lot of leeway when it comes to the implementation - in fact, coming up with a basic distance function takes just a couple lines of code:
type DistFn = Box<dyn Fn(Date) -> Span>; fn compile_recur(recur: &Recur) -> DistFn { Box::new(move |curr: Date| -> Span { // Check if `curr` matches any of the `BYDAY` rules // (evaluates to `true` if `by_day` is empty) let matches_by_day = recur.by_day.iter().any(|wd| { curr.weekday() == wd }); // Check if `curr` matches any of the `BYMONTHDAY` rules // (evaluates to `true` when `by_month_day` is empty) let matches_by_month_day = recur.by_month_day.iter().any(|md| { curr.month_day() == md }); /* ... */ let matches_all = matches_by_day && matches_by_month_day && /* ... */; if matches_all { // If all of the rules are satisfied, great! -- return zero, since // this date must be an occurrence of the underlying event. Span::zero() } else { // If any of the rules don't match, return a guess as to when the // next occurrence might be. We can underapproximate, but we can't // overshoot, so let's take an epsilon of one second - can't go // wrong with it! // // (that's because recurrence rules don't support milliseconds - a // second is the lowest unit.) Span::seconds(1) } }) }
Now that we have this magical thing available, what can we do with it? We march!
fn iter( dist: DistFn, dtstart: Date, ) -> impl Iterator<Item = Date> { // Start at the first date at which the event repeats let mut curr = dtstart; loop { // Call the distance function and note down the step size let step = dist(curr); // If step is zero, it means that `curr` is a repetition of `event` - // in that case we can just yield it back to the caller. // // Conversely, a non-zero step tells us how we can get closer to the // next occurrence; not necessarily directly at it, just closer. if step.is_zero() { yield curr; // As compared to ray marching, in here we're interested not in // the first occurrence, but in *all* of them - so having reached // a `dist`s root, let's add an arbitrarily small span to get the // ball rolling again in the next iteration. // // Without this, the next iteration would yield `curr` back again, // forever, since `step` is zero. curr += Span::seconds(1); } else { curr += step; } } }
hey, that's stupid, you're just iterating over all possible dates
You're right! What we've got so far is essentially:
fn iter( recur: &Recur, dtstart: Date, ) -> impl Iterator<Item = Date> { let mut curr = dtstart; loop { if recur.matches(curr) { yield candidate; } curr += Span::seconds(1); } }
... which is stupid - for instance given:
FREQ=DAILY;BYSECOND=0,10,20;DTSTART=20180101T120000
... the algorithm will do:
curr = 2018-01-01 12:00:00
iteration 1:
# 12:00:00 matches BYSECOND=0,10,20
yield curr
curr += 1 second
iteration 2:
# 12:00:01 doesn't match BYSECOND=0,10,20
curr += 1 second
iteration 3:
# 12:00:02 doesn't match BYSECOND=0,10,20
curr += 1 second
iteration 4:
# 12:00:03 doesn't match BYSECOND=0,10,20
curr += 1 second
/* ... */
iteration 11:
# 12:00:10 matches BYSECOND=0,10,20
yield curr
curr += 1 second
... and that's a lot of iterations, I agree - but the important bit is that the outcome is correct.
It's inefficient, yes - but correct. This means that our approach is sound, we just need to find a way to make it more efficient, more practical; we need to optimize it.
Of course, we also have to implement more rules, e.g. conveniently
enough we've skipped how the FREQ rule is supposed to
work, but no worries - we'll get there.
Atoms
Let's ignore time for a moment. Nooo time. Zero. Null. Bliss. Remember that time Jeff has said something mean to you? No, you don't, because there's no time.
Uhm, anyway. Let's focus on day-dates, such as
2018-01-01 - say we're given the following rule:
FREQ=DAILY;BYDAY=MO,TU;BYMONTHDAY=10;DTSTART=20180101
... which corresponds to this pseudo-SQL:
select day from dates where day_of_week(day) = 'Monday' or day_of_week(day) = 'Tuesday' and day_of_month(day) = 10 and day >= '2018-01-01'
How do we get from here towards a good distance function? Piecewise.
Let's tackle day_of_week first.
Ignoring the context in which it appears, how would we like for
an ideal day-of-week distance function to work? We can
come up with a couple of examples:
(day-of-week Monday 2018-01-01) = 0 // 2018-01-01 is Monday (day-of-week Tuesday 2018-01-01) = +1d // 2018-01-01 one day away from Tuesday (day-of-week Friday 2018-01-01) = +5d // 2018-01-01 five days away from Friday
Since we don't care about travelling back in time, we can also state that:
(day-of-week Monday 2018-01-02) = +6d // 2018-01-02 is technically -1d away from the nearest Monday (2018-01-01), // but since we want for the returned spans to be positive, let's choose the // next Monday (2018-01-08), which is +6d away from 2018-01-02
Now that we have a couple of examples, it's time to come up with an implementation - we'll use Jiff as the base for our algorithm, since I've already had a chance to play with it and it's very pleasant.
Before we jump into the code, there's one thing we're going to
simplify - instead of juggling fn(Date) -> Span, we'll go
ahead with fn(Date) -> Date, where the
span.is_zero() condition is encoded as the function
returning the same date as the input one:
(day-of-week Monday 2018-01-01) = 2018-01-01 (day-of-week Tuesday 2018-01-01) = 2018-01-02 (day-of-week Friday 2018-01-01) = 2018-01-05
This doesn't really change anything, we're just making our lives easier, because in practice working on dates tends to be easier than working on spans. Without further ado:
use jiff::Span; use jiff::civil::{Date, Weekday}; enum Rule { DayOfWeek(Weekday), } impl Rule { fn next(&self, curr: Date) -> Date { match self { Rule::DayOfWeek(wd) => { curr + Span::new().days(curr.weekday().until(*wd)) } } } }
That wasn't so hard, was it? We can confirm it's working as intended:
#[cfg(test)] mod tests { use super::*; #[track_caller] fn date(s: &str) -> Date { s.parse().unwrap() } #[test] fn day_of_week() { assert_eq!( date("2018-01-01"), Rule::DayOfWeek(Weekday::Monday) .next(date("2018-01-01")) ); assert_eq!( date("2018-01-02"), Rule::DayOfWeek(Weekday::Tuesday) .next(date("2018-01-01")) ); assert_eq!( date("2018-01-05"), Rule::DayOfWeek(Weekday::Friday) .next(date("2018-01-01")) ); assert_eq!( date("2018-01-08"), Rule::DayOfWeek(Weekday::Monday) .next(date("2018-01-02")) ); } }
Ok, so it seems distance functions are not as scary as they seem! Or at least this one isn't, but I can tell you that most of them will be similarly intuitive.
Moving on to day-of-month - as before, first let's
imagine how we'd like for it to behave:
(day-of-month 14 2018-01-14) = 2018-01-14 // 2018-01-14 is already the 14th day of month (day-of-month 16 2018-01-14) = 2018-01-16 // 2018-01-16 is the closest 16th day of month starting from 2018-01-14 (+2d) (day-of-month 12 2018-01-14) = 2018-02-12 // 2018-01-12 is the closest 12th day of month starting from 2018-01-14 (-2d), // but that corresponds to a negative span, so we jump to the next month
Implementing this one is a bit more tricky, but not dangerously so - there are three edge cases:
/* ... */ use std::cmp::Ordering; enum Rule { /* ... */ DayOfMonth(i8), } impl Rule { fn next(&self, curr: Date) -> Date { match self { /* ... */ Rule::DayOfMonth(day) => { match curr.day().cmp(day) { // E.g. curr=2018-01-14 and day=16 Ordering::Less => todo!(), // E.g. curr=2018-01-14 and day=14 Ordering::Equal => todo!(), // E.g. curr=2018-01-14 and day=12 Ordering::Greater => todo!(), } } } } }
... out of which the Less and Equal branches
are pretty straightforward:
match self { /* ... */ Rule::DayOfMonth(day) => { match curr.day().cmp(day) { // E.g. curr=2018-01-14 and day=16 Ordering::Less => curr + Span::new().days(day - curr.day()), // E.g. curr=2018-01-14 and day=14 Ordering::Equal => curr, // E.g. curr=2018-01-14 and day=12 Ordering::Greater => todo!(), } } }
What about => Ordering::Greater? Well, we could provide
an exact solution:
// E.g. curr=2018-01-14 and day=12 Ordering::Greater => { // 2018-01-14 -> 2018-02-14 let dst = curr + Span::months(1); // 2018-02-14 -> 2018-02-01 let dst = dst.first_of_month().unwrap(); // 2018-02-01 -> 2018-02-12 dst + Span::days(*day - 1) }
... but since it's legal to underapproximate, we might as well go the easier way:
Ordering::Greater => curr.last_of_month().tomorrow().unwrap(),
Given curr=2018-01-14 and day=12, the
function will suggest jumping to 2018-02-01 and then, on
the next iteration, we'll hit the Less branch to end up
on 2018-02-12. Somewhat inefficient, but legal.
Ok, we've got day-of-week, we've got
day-of-month - time for conditionals!
Yield Me Maybe
There are two types of boolean operators we need to support,
or and and. or is used for
combining values for the same parameter, while
and combines across parameters:
(and (or (day-of-week Monday) (day-of-week Tuesday)) (day-of-month 10))
... or, a bit less LISP-y:
(day-of-week(Monday) or day-of-week(Tuesday)) and day-of-month(10)
What does it mean
day-of-week(Monday) or day-of-week(Tuesday), then?
Pessimistically, it's like:
if day-of-week(Monday) == 0 or day-of-week(Tuesday) == 0:
return 0
else
return +1s
... i.e. we march, slowly, looking for any of the functions to return zero. We know that marching second-by-second is legal, just suboptimal, so now the question becomes - how do we do it better?
Our functions have this nice property that:
if:
f(x) = y
then, for t >= 0 && x + t <= y:
f(x + t) = y
This means that f(x) or g(x) corresponds to
min(f(x), g(x)), which we can eyeball by doing:
since 2018-01-03 is Wednesday, we'd expect for the next ocurrences to be: -> 2018-01-08 (Monday, since it comes before the next Tuesday) -> 2018-01-09 (Tuesday, since it comes before the next Monday) -> 2018-01-15 (Monday, ...) -> [...]
This boils down to the following cute snippet:
enum Rule { /* ... */ Or(Vec<Self>), } impl Rule { fn next(&self, curr: Date) -> Date { match self { /* ... */ Rule::Or(rules) => { rules .iter() .map(|rule| rule.next(curr)) .min() .unwrap_or(curr) } } } }
Conversely, and = max, for a similar reason: if
f(x) says it won't be valid until some date
A and g(x) says it won't be valid until some
date B, then both won't be valid until at least
max(A, B).
This doesn't necessarily mean that both rules are valid at
max(A, B), e.g.:
(and (day-of-week Monday) (day-of-month 10)) Given 2018-01-03, we'll evaulate: (day-of-week Monday 2018-01-03) = 2018-01-08 (day-of-month 10 2018-01-03) = 2018-01-10 (and (day-of-week ...) (day-of-month ...)) = (max 2018-01-08 2018-01-10) = 2018-01-10 2018-01-10 isn't Monday though, so we have to try again on the next iteration.
Still, and = max is alright, because it's legal to
underapproximate:
enum Rule { /* ... */ And(Vec<Self>), } impl Rule { fn next(&self, curr: Date) -> Date { match self { /* ... */ Rule::And(rules) => { rules .iter() .map(|rule| rule.next(curr)) .max() .unwrap_or(curr) } } } }
Molecules
We're still missing the FREQ rule, but what we've got so
far is sufficient to play with:
/* ... */ use std::iter; struct Recur { by_day: Vec<Weekday>, by_month_day: Vec<i8>, dtstart: Date, } impl Recur { fn as_rule(&self) -> Rule { let mut rules = Vec::new(); // If BYDAY paremeter is present, emit the DayOfWeek rule if !self.by_day.is_empty() { rules.push(Rule::Or( self.by_day .iter() .copied() .map(Rule::DayOfWeek) .collect(), )); } // If BYMONTHDAY parameter is present, emit the DayOfMonth rule if !self.by_month_day.is_empty() { rules.push(Rule::Or( self.by_month_day .iter() .copied() .map(Rule::DayOfMonth) .collect(), )); } Rule::And(rules) } fn iter(&self) -> impl Iterator<Item = Date> { let rule = self.as_rule(); let mut curr = self.dtstart; iter::from_fn(move || { loop { let next = rule.next(curr); if next == curr { curr += Span::new().days(1); break Some(next); } else { curr = next; } } }) } }
... and voilà:
#[cfg(test)] mod tests { /* ... */ #[test] fn smoke() { // FREQ=DAILY;BYDAY=MO,TU;BYMONTHDAY=10,20,30;DTSTART=20180101 let recur = Recur { by_day: vec![Weekday::Monday, Weekday::Tuesday], by_month_day: vec![10, 20, 30], dtstart: date("20180101"), }; let actual: Vec<_> = recur.iter().take(5).collect(); // Cross-checked with https://jkbrzt.github.io/rrule let expected = vec![ date("2018-01-30"), date("2018-02-20"), date("2018-03-20"), date("2018-04-10"), date("2018-04-30"), ]; assert_eq!(expected, actual); } /* ... */ }
Now, I could go on and implement all of the other parameters, but for
the most part they follow the outline showed here, nothing fancy - so
instead let's wrap up by implementing the parameters that require a
bit different approach,
FREQ and INTERVAL.
The simplest case is the default of INTERVAL=1 - it feels
quite intuitive, but what does it really mean?
Let's analyze a specific example:
-> 2018-01-14 -> 2018-02-14 -> 2018-03-14 -> 2018-04-14 -> [...]
What's the pattern? Perhaps surprisingly, we can already encode it -
that's just (day-of-month 14)!
This means that
FREQ=MONTHLY;INTERVAL=1;DTSTART=201801014 is really
BYMONTHDAY=14;DTSTART=20180114 - and actually all forms
of FREQ=;INTERVAL=1 can be reduced to some combination of
the BY* rules:
FREQ=YEARLY;INTERVAL=1;DTSTART=20180114 -> BYMONTH=1;BYMONTHDAY=14 -> (and (month 1) (day-of-month 14))
FREQ=MONTHLY;INTERVAL=1;DTSTART=20180114 -> BYMONTHDAY=14 -> (day-of-month 14)
FREQ=WEEKLY;INTERVAL=1;DTSTART=20180114 -> BYDAY=SU -> (weekday Sunday)
FREQ=DAILY;INTERVAL=1;DTSTART=20180114 -> no-op
What about intervals larger than one? Once again, let's take an example:
-> 2018-01-14 -> 2018-06-14 -> 2018-11-14 -> 2019-04-14 -> [...]
... or two, to have a complete picture:
-> 2018-01-15 -> 2018-01-16 -> 2018-01-22 -> 2018-01-23 -> 2018-01-29 -> 2018-01-30 -> 2018-06-04 -> 2018-06-05 -> [...]
Alright, what's the pattern? Looking at the first example suggests:
date = DTSTART + FREQ * INTERVAL * nth -> 2018-01-14 = 2018-01-14 + 5 months * 0 -> 2018-06-14 = 2018-01-14 + 5 months * 1 -> 2018-11-14 = 2018-01-14 + 5 months * 2 -> 2019-04-14 = 2018-01-14 + 5 months * 3
... but this falls apart over the second example where none of the dates are an exact repetition:
-> 2018-01-15 = 2018-01-14 + 1 day -> 2018-01-16 = 2018-01-14 + 2 days -> [...] -> 2018-06-04 = 2018-01-14 + 4 months and 21 days -> 2018-06-05 = 2018-01-14 + 4 months and 22 days -> [...]
In fact, 2018-06-04 isn't even 5 months apart from
2018-01-14!
If we're not literally repeating the starting date, then what's going
on? Let's compare a correct and an incorrect occurrence, following the
second example and ignoring BYDAY=MO,TU for a moment:
correct: -> 2018-06-04 = 2018-01-14 + 4 months and 21 days incorrect: -> 2018-05-31 = 2018-01-14 + 4 months and 17 days
Clearly we're doing something wrong by looking the distance between
DTSTART and our candidate. In particular, we can see that
DTSTART's day part doesn't affect anything, except for in
the first month.
That is, if we started on DTSTART=20180120, we'd still go
through 2018-06-04, even though the distance between
those two just got shorter - so for FREQ=MONTHLY we
should have a way of comparing dates that ignores the day part.
One approach could be:
fn months_of(date: Date) -> i16 { date.year() * 12 + date.month() } fn months_between(lhs: Date, rhs: Date) -> i16 { months_of(lhs) - months_of(rhs) } // ... and then we make sure that months_between() is divisible by INTERVAL
... but Jiff's spans are more convenient to work with, and they generalize to other units as well:
/* ... */ use jiff::{SpanRound, Unit}; /* ... */ enum Rule { /* ... */ InstanceOf(Date, Unit, i32), /* ... */ } impl Rule { fn next(&self, curr: Date) -> Date { match self { /* ... */ Rule::InstanceOf(start, unit, interval) => { // Calculate the distance between `start` and our candidate // date (`curr`). // // `start` is expected to be already snapped to the first day // of month, first day of year etc. let diff = curr.since(*start).unwrap(); // By default `.since()` returns span in days - for proper // comparison we need to round it to months, years etc. let diff = diff .round( SpanRound::new() .largest(*unit) .relative(*start) ) .unwrap(); // Now we've got all the funny numbers we need! match unit { Unit::Month => { let diff = diff.get_months() % interval; if diff == 0 { curr } else { (curr + Span::new().months(interval - diff)) .first_of_month() } } _ => todo!(), } } /* ... */ } } }
This new rule integrates quite nicely with the existing code:
enum Freq { Daily, Monthly, Yearly, } struct Recur { freq: Freq, interval: i32, by_day: Vec<Weekday>, by_month_day: Vec<i8>, dtstart: Date, } impl Recur { fn as_rule(&self) -> Rule { let mut rules = Vec::new(); // Create the `InstanceOf` rule rules.push({ // Snap `start` to the beginning of `FREQ` let start = match self.freq { Freq::Daily => self.dtstart, Freq::Monthly => self.dtstart.first_of_month(), Freq::Yearly => todo!(), }; // Convert our `Freq` into Jiff's `Unit` let unit = match self.freq { Freq::Daily => Unit::Day, Freq::Monthly => Unit::Month, Freq::Yearly => Unit::Year, }; Rule::InstanceOf(start, unit, self.interval) }); /* ... */ // Create implied rules match self.freq { Freq::Daily => { // No extra rules required } Freq::Monthly => { if self.by_day.is_empty() && self.by_month_day.is_empty() { rules.push(Rule::DayOfMonth(self.dtstart.month())); } } Freq::Yearly => { todo!("left as an exercise for the reader"); } } Rule::And(rules) } }
... and voilà:
#[cfg(test)] mod tests { /* ... */ #[test] fn smoke() { // FREQ=MONTHLY;INTERVAL=5;BYDAY=FR;DTSTART=20180114 let recur = Recur { freq: Freq::Monthly, interval: 5, by_day: vec![Weekday::Friday], by_month_day: Vec::new(), dtstart: date("20180119"), }; // Cross-checked with https://jkbrzt.github.io/rrule let actual: Vec<_> = recur.iter().take(8).collect(); let expected = vec![ date("2018-01-19"), date("2018-01-26"), date("2018-06-01"), date("2018-06-08"), date("2018-06-15"), date("2018-06-22"), date("2018-06-29"), date("2018-11-02"), ]; assert_eq!(expected, actual); } }
As it turns out, spooky RFC tables don't have to always end up in spooky code!
Closing thoughts
Isn't it too complex?
I'd argue that this distance-based approach is actually simpler than what other implementations do.
That's because at every step you have something that's easy to reason about in isolation - you have one function that rounds date to the next week, you have another function that takes two values and returns the smallest one etc., and all of those functions make sense on their own.
Not to mention that fast-forwarding - "find me the next occurrence after xxx" - is something that other implementations struggle with, while in this case you get it for free.
Isn't it too slow?
Seems to be okay - I've benchmarked my reasonably optimized implementation (closed source for the time being) and iterating hundreds of times over complex rules happens under a millisecond.
The beauty of going distancefunctioned™ is that you can optimize as much or as little as you want - after all, half of this article is actually spent talking about optimization.
Surely you can't be the first one to come up with this?
I hope I'm not the first one! I couldn't find any existing implementation that works this way, though.
The mathematical foundation also escapes me - surely this must've been already discovered in one form or another, but I haven't found anything this specific.
Proximal operator sounds quite close; Frank-Wolfe maybe? If you have an idea, lemme know!