Learning to Fly: Let's simulate evolution in Rust (pt 1)
This post is part of the learning-to-fly series:
In this series we'll create a simulation of evolution using neural network and genetic algorithm.
I'm going to introduce you to how a basic neural network and genetic algorithm works, then we'll implement both in Rust and compile our application to WebAssembly to ultimately end up with:
This series will be divided into a few posts, roughly:
-
Introduction to the domain (what are we going to simulate, how does a neural network & genetic algorithm work),
-
Implementing a neural network,
-
Implementing a genetic algorithm,
-
Implementing eyes, brain and the simulation itself.
Curious? Hop on the bus, Gus, and onto the first chapter: Design.
Design
Let's start by clearly defining our objective: what are we going to simulate, actually?
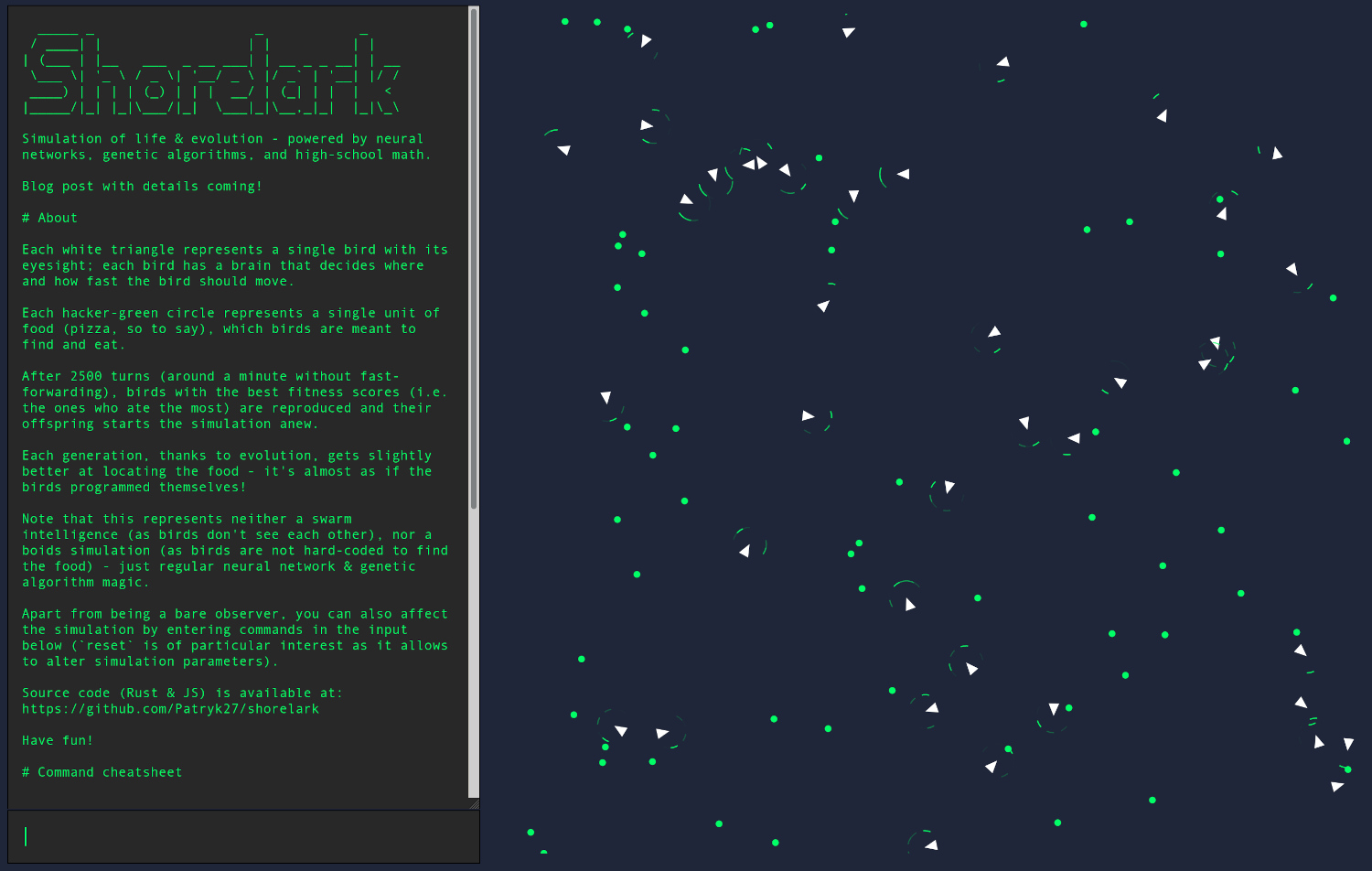
The overall idea is that we have a two-dimensional board representing a world:
This world consists of birds (hence the project's original code name - Shorelark):
... and foods (of an abstract kind, rich in protein & fiber):
Each bird has their own vision, allowing them to locate the food:
... and a brain that controls bird's body (i.e. speed and rotation).
Our magic touch will lay in the fact that instead of hard-coding our birds to some specific behavior (e.g. "go to the nearest food in your eyesight"), we'll take a more interesting route:
We'll make our birds able to learn and evolve.
Brain
If you squint your eyes hard enough, you'll see that a brain is nothing but a function of some inputs to some outputs, e.g.:
Since our birds will have only one sensory input, their brains can be then approximated as:
Mathematically, we can represent this function's input (i.e. biological eye) as a list of numbers, with each number (i.e. biological photoreceptor) describing how close the nearest object (i.e. food) is:
(0.0 - no object in sight, 1.0 - object
right in front of us.)
As for the output, we'll make our function return a tuple of
(Δspeed, Δrotation).
For instance, a brain telling us (0.1, 45) will mean
"body, please increase our speed by 0.1 units and rotate
us 45 degrees clockwise", while
(0.0, 0) will mean "body, please keep our course steady".
Finally, let's address the elephant in the room: so a brain is
basically
f(eyes), right? But how do we find out what actually
follows the equals sign?
f(eyes) = what?
Neural network: Introduction
As a fellow human, you might be aware that brains are made of neurons connected via synapses:
Synapses carry electric and chemical signals between neurons, while neurons "decide" whether given signal should be propagated further or stopped; eventually this allows for people to recognize letters, eat brussels sprouts, and write mean comments on Twitter.
Due to their inherent complexity, biological neural networks are not among the easiest to simulate (one could argue that neurons are thus not Web Scale), which made some smart people invent a class of mathematical structures called artificial neural networks, which allow to approximate - with a pinch of salt - brain-like behavior using math.
Artificial neural networks (which I'm going to call just neural networks) are prominent at generalizing over datasets (e.g. learning how a cat looks like), so they found their use in face recognition (e.g. for cameras), language translation (e.g. for GNMT), and - in our case - to steer colorful pixels for a handful of Reddit karma.
The particular kind of network we'll be focusing on is called
feedforward neural network (FFNN)…
... and it looks like this:
This is a layout of an FFNN with five synapses and three neurons, all organized in two layers: the input layer (on the left side) and the output layer (on the right side).
There may also exist layers in-between, in which case they are called hidden layers - they improve the network's ability to understand the input data (think: the bigger the brain, the "more abstraction" it might understand, to a certain degree).
Contrary to biological neural networks (which piggyback on electric signals), FFNNs work by accepting some numbers at their input and propagating (feedforwarding) those numbers layer-by-layer across the entire network; numbers that appear at the last layer determine network's answer.
For instance, if you fed your network with raw pixels of a picture, you might've got a response saying:
-
0.0- this picture does not contain an orange cat eating lasagna, -
0.5- this picture might contain an orange cat eating lasagna, -
1.0- this picture certainly contains an orange cat eating lasagna.
It's also possible for a network to return many values (the number of output values is equal to the number of neurons in the output layer):
-
(0.0, 0.5)- this picture does not contain an orange cat, but might contain a lasagna, -
(0.5, 0.0)- this picture might contain an orange cat, but does not contain a lasagna.
The meaning of input and output numbers is up to you - in this case we've simply imagined that there exists some neural network behaving this way, but in reality it's on you to prepare so-called training dataset ("given this picture, you should return 1.0", "given that picture, you should return 0.0").
Having the general overview of FFNNs in mind, let's now take the next major step and learn about the magic allowing for all of this to happen.
Neural network: Deep dive
FFNNs lean on two building blocks: neurons and synapses.
A neuron (usually represented with a circle) accepts some input values, processes them and returns some output value - each neuron has at least one input and at most one output:
Additionally, each neuron has a bias:
Bias is like a neuron's if statement - it allows for a
neuron to stay inactive (return an output of zero) unless> the input
is strong (high) enough. Formally we'd say that bias allows to
regulate neuron's activation threshold.
Imagine you've got a neuron with three inputs, with each input
determining whether it sees a lasagna (1.0) or not
(0.0) - now, if you wanted to create a neuron that's
activated when it sees at least two lasagnas, you'd simply
create a neuron with a bias of -1.0; this way your
neuron's "natural" state would be -1.0 (inactive), with
one lasagna - 0.0 (still inactive), and with two -
1.0 (active, voilà).
Apart from neurons, we've got synapses - a synapse is like a wire that connects one neuron's output to another neuron's input; each synapse is of certain weight:
A weight is a factor (hence the x before each number, to
emphasize its multiplicative nature), so a weight of:
-
0.0means that a synapse is effectively dead (it doesn't pass any information from one neuron into the another), -
0.3means that if neuron A returns0.7, neuron B will receive0.7 * 0.3 ~= 0.2, -
1.0means that a synapse is effectively passthrough - if neuron A returns0.7, neuron B will receive0.7 * 1.0 = 0.7.
Having all this knowledge in mind, let's go back to our network and fill-in missing weights & biases with some random numbers:
What a beauty, isn't it?
Let's see what it thinks of, say, (0.5, 0.8):
To reiterate, we're interested in the output value of the rightmost neuron (that's our output layer) - since it depends on two previous neurons (the ones from the input layer), we're going to start with them.
Let's focus on the top-left neuron first - to calculate its output, we start by computing a weighted sum of all its inputs:
0.5 * 0.2 = 0.1
... then, we add the bias:
0.1 - 0.3 = -0.2
... and clamp this value through so-called
activation function; activation function limits neuron's output
to a predefined range, simulating the if-like behavior.
The simplest activation function is
rectified linear unit (ReLU), which is basically
f32::max:
As you can see, when our weighted-sum-with-a-bias is lower than zero,
the neuron's output will be 0.0 - and that's exactly what
happens to our current output:
max(-0.2, 0.0) = 0.0
Nice; now let's do the bottom-left one:
# Weighted sum: 0.8 * 1.0 = 0.8 # Bias: 0.8 + 0.0 = 0.8 # Activation function: max(0.8, 0.0) = 0.8
At this point we've got the input layer completed:
... which heads us towards the last neuron:
# Weighted sum: (0.0 * 0.6) + (0.8 * 0.5) = 0.4 # Bias: 0.4 + 0.2 = 0.6 # Activation function: max(0.6, 0.0) = 0.6
... and the network's output itself:
0.6 * 1.0 = 0.6
Voilà - for the input of (0.5, 0.8), our network
responded 0.6.
(since it's just an exercise on a totally made-up network, this number doesn't mean anything - it's just some output value.)
Overall, that's one of the simplest FFNNs possible - given appropriate weights, it's able to solve the XOR problem, but probably lacks the capacity to steer a bird.
More complex FFNNs, such as this one:
... work exactly the same way: you just go left-to-right, neuron-by-neuron, computing the outputs, until you squeeze all the numbers from the output layer.
(on that particular diagram some of the synapses overlap, but it doesn't mean anything: it's just that representing multidimensional graphs on a flat screen is unfortunate.)
At this point you might begin to wonder "wait, how do we know our network's weights?", and for that I've got a simple answer:
we randomize them! ❤️️
If you're accustomed to deterministic algorithms (bubble sort, anyone?), this might feel itchy to you, but it's the way things go for networks containing more than a few neurons: you cross your fingers, randomize the initial weights and work with what you got.
Notice I said initial weights - having some non-zero weights in place, there are certain algorithms that you can apply on your network to improve it (so, essentially, to teach it).
One of the most popular "teaching" algorithms for FFNNs is backpropagation:
You show your network lots (think: hundredths of thousands) of examples in the form of "for this input, you should return that" (think: "for this picture of dakimakura, you should return pillow") and backpropagation slowly adjusts your network's weights until it gets the answers right.
Backpropagation is a great tool if you have a rich set of labeled examples (such as photos or statistics) and that's why it doesn't fit our original assumption:
We ain't no statisticians, the world is a cruel place, so we want for our birds to figure out all the learning on their own (contrary to being given concrete examples of "for this vision, go left", "for this vision, go right").
Solution?
biology genetic algorithms and the magic of
large numbers
Genetic algorithm: Introduction
To recap, from the mathematical point of view our underlying problem is that we have a function (represented using a neural network) that's defined by a whole lot of parameters:
(I didn't bother to draw all the weights, but I hope you get the point - there's a lot of them.)
Had we represented each parameter with a single-precision floating-point number, a network of mere 3 neurons and 5 synapses could be defined in so many different combinations…
(3.402 * 10^38) ^ (3 + 5) ~= 1.8 * 10^308
( how-many-floating-point-numbers-are-there )
... that the universe would sooner meet its ultimate fate than we'd be done checking them all - we certainly need to be smarter!
Since iterating through our search space looking for the single best answer is off the table, we can focus on a much simpler task of finding a list of suboptimal answers.
And in order to do that, we must dig deeper.
Genetic algorithm: Deep dive
This is a wild carrot together with its domesticated form:

This domesticated, widely known form didn't appear out of blue - it's an outcome of hundredths of years of selective breeding with certain factors - like taproot's texture or color - in mind.
Wouldn't it be awesome if we could do a similar thing with our neural brains? If we just, like, created a bunch of random birds and selectively bred the ones which seemed the most prominent…
hmmm
As it turns out, we're not the first to stumble upon this idea - there already exists a widely researched branch of computer science called evolutionary computation that's all about solving problems "just the way nature would do".
Out of all the evolutionary algorithms, the concrete subclass we'll be studying is called genetic algorithm.
Starting top-bottom, a genetic algorithm starts with a population:
A population is built from individuals (sometimes called agents):
An individual (or an agent) is a single possible solution to given problem (a population is thus a set of possible solutions).
In our case, each individual will model a brain (or an entire bird, if you prefer to visualise it this way), but generally it depends on the problem you're tackling:
-
If you were trying to, say, evolve an antenna, a single individual would be a single antenna.
-
If you were trying to, say, evolve a query plan, a single individual would be a single query plan.
An individual is built from genes (collectively named genome):
A gene is a single parameter that's being evaluated and tuned by the genetic algorithm.
In our case, each gene will be simply a neural network's weight, but representing problem's domain isn't always this straightforward.
For instance, if you were trying to
help a fellow salesman, where the underlying problem isn't based on neural networks at all,
a single gene could be a tuple of (x, y) coordinates
determining a part of the salesman's journey (consequently, an
individual would then describe the salesman's entire path):
Now, let's say we've got a random population of fifty birds - we pass them to a genetic algorithm, what happens?
Similarly as with selective breeding, genetic algorithm starts by evaluating each of the individuals (each of the possible solutions) to see which are the best among the current population.
Biologically, this is an equivalent of taking a stroll to your garden and checking which carrots are the orangest and the yummiest.
Evaluation happens using so-called fitness function that returns a fitness score quantifying how good a particular individual (so a particular solution) is:
Creating a usable fitness function is one of the hardest tasks when it comes to genetic algorithms, as usually there are many metrics by which an individual can be measured.
(even our imaginative carrot has at least three metrics: taproot's color, radius and taste, and they all have to be squashed into a single number.)
Fortunately, when it comes to birds, we don't have much to choose from anyway: we'll just say that a bird is as good as the amount of food it ate during the course of the current generation.
A bird who ate 30 foods is better than the one who ate
just 20, simple as that.
Now, the time has come for the genetic algorithm's crème de la crème: reproduction!
Broadly speaking, reproduction is the process of building a new (hopefully - slightly improved) population starting from the current one.
It's the mathematical equivalent of choosing the tastiest carrots and planting their seeds.
What happens is that the genetic algorithm chooses two individuals at random (prioritizing the ones with the higher fitness scores) and uses them to produce two new individuals (a so-called offspring):
Offspring is produced by taking genomes of both parents and performing crossover and mutation on them:
Both newly-spawned individuals are pushed into the pool of
new population and the process starts over until the
entire new population is built; the current population then gets
discarded and the whole simulation starts over on this new (hopefully
improved!) population.
As you can see, there's a lot of randomness in the process: we start with a random population, we randomize how the genes are being distributed… so…
this cannot actually work, can it?