Learning to Fly: Let's simulate evolution in Rust (pt 2)
This post is part of the learning-to-fly series:
This is the second part of the Learning to Fly series in which we're coding a simulation of evolution using neural network and genetic algorithm:
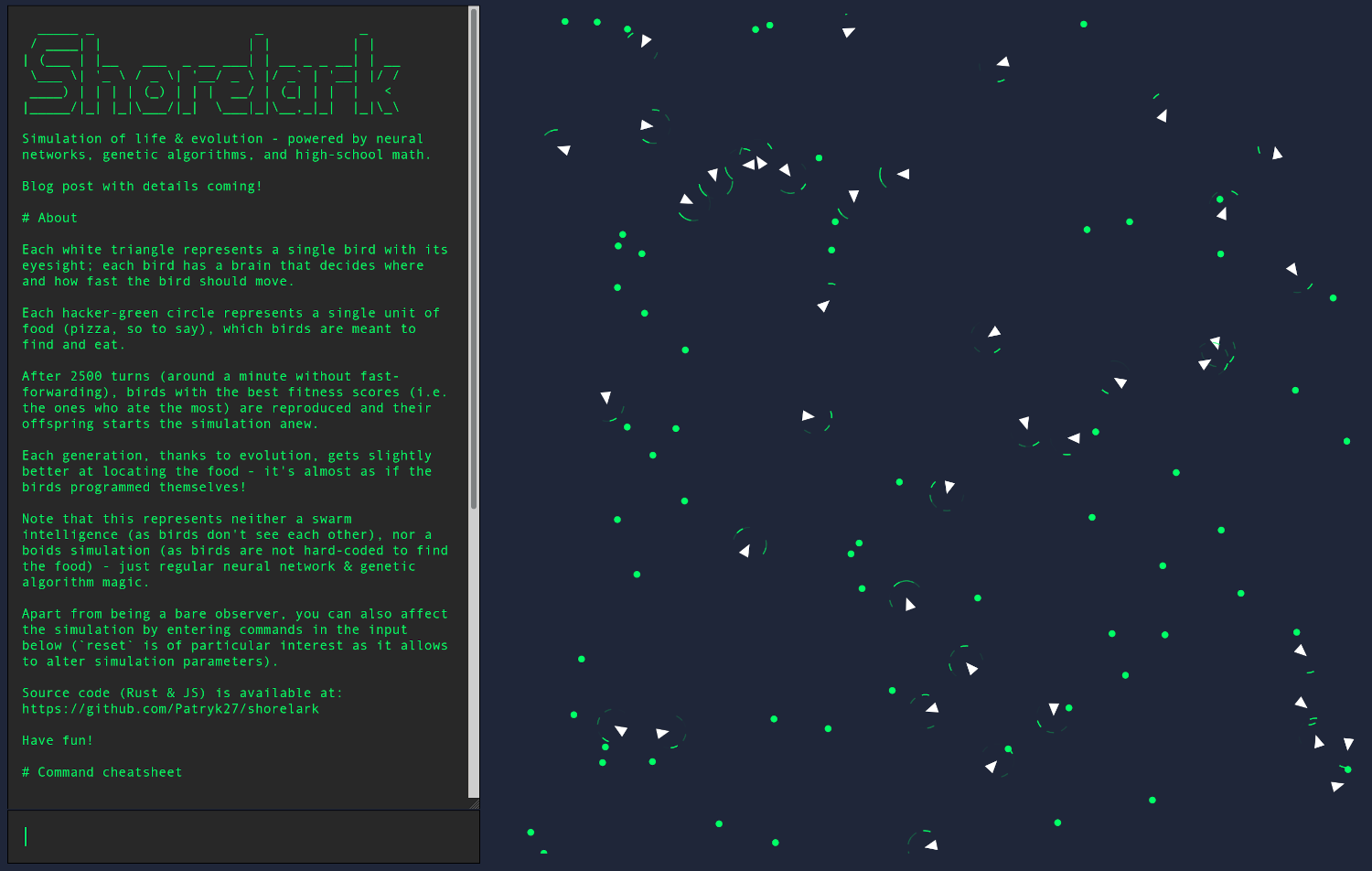
In this post we'll lay the foundations for our project and implement a basic feed-forward neural network that'll later become a brain; we'll also take a look at many intricacies and idioms you might find in common Rust code, including in tests.
Strap your straps, seatbelt your seatbelts and get ready for some coding!
Setup
Oh, the joys of starting a new project!
$ mkdir shorelark $ cd shorelark # If you're using Git, it's also the time for: $ git init
First things first, we have to establish which toolchain version we'll be using - otherwise, if you happened to have an older toolchain installed, some parts of the code could not work for you.
As of March 2024, the latest stable version of Rust is 1.76, so let's
go ahead and create a file called rust-toolchain that
says:
1.76.0
Phew!
Now, for the more difficult part - we have to decide how our project's structure will look like. Because our project will consist of many independent submodules (such as the neural network and genetic algorithm), a workspace will come handy:
[workspace] resolver = "2" members = [ "libs/*", ]
What this means is that instead of having
src/main.rs right away, we'll create a directory called
libs and put our hand-written libraries (aka
crates) in there:
$ mkdir libs $ cd libs $ cargo new neural-network --name lib-neural-network --lib
Coding: propagate()
It's time to get down to business.
We'll start top-down, with a structure modelling the entire
network - it will provide an entry point to our crate; let's
open lib.rs and write:
#[derive(Debug)] pub struct Network;
A neural network's most crucial operation is propagating numbers:
... so:
#[derive(Debug)] pub struct Network; impl Network { pub fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> { todo!() } }
Similarly to an ocean filled with droplets, a network is built from layers:
... so:
#[derive(Debug)] pub struct Network { layers: Vec<Layer>, } #[derive(Debug)] struct Layer;
Layers are built from neurons:
... giving us:
#[derive(Debug)] struct Layer { neurons: Vec<Neuron>, }
Eventually, neurons contain biases and output weights:
#[derive(Debug)] struct Neuron { bias: f32, weights: Vec<f32>, }
Let's see our initial design in its entriety:
#[derive(Debug)] pub struct Network { layers: Vec<Layer>, } impl Network { pub fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> { todo!() } } #[derive(Debug)] struct Layer { neurons: Vec<Neuron>, } #[derive(Debug)] struct Neuron { bias: f32, weights: Vec<f32>, }
Nice.
Next, since numbers have to be shoved through each layer, we'll need
to have a
propagate() in there, too:
impl Layer { fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> { todo!() } }
Having Layer::propagate(), we can go back and implement
Network::propagate():
impl Network { pub fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> { let mut inputs = inputs; for layer in &self.layers { inputs = layer.propagate(inputs); } inputs } }
This is quite a satisfying, correct piece of code - but it's also non-idiomatic - we can write it better, more rustic; let's see how!
First of all, this is called a rebinding (or shadowing):
let mut inputs = inputs;
... and it's unnecessary, because we might as well move this
mut into the function's parameter:
impl Network { pub fn propagate(&self, mut inputs: Vec<f32>) -> Vec<f32> { for layer in &self.layers { inputs = layer.propagate(inputs); } inputs } }
There's one more refinement we can apply to our code - this very pattern is known as folding:
for layer in &self.layers { inputs = layer.propagate(inputs); }
... and Rust's standard library provides a dedicated function for it:
impl Network { pub fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> { self.layers .iter() .fold(inputs, |inputs, layer| layer.propagate(inputs)) } }
(one could argue whether our final code is actually more readable or
less - while I'm fond of the built-in combinators such as
.fold(), if you find them obscure - that's fine, you do
you!)
Voilà - after all, thanks to the closure, we didn't even need that
mut inputs - now you can brag about your code being all
functional and Haskell-y.
Let's move on to neurons - a single neuron accepts many inputs and returns a single output, so:
#[derive(Debug)] struct Neuron { bias: f32, weights: Vec<f32>, } impl Neuron { fn propagate(&self, inputs: Vec<f32>) -> f32 { todo!() } }
As before, we can backtrack to implement
Layer::propagate():
#[derive(Debug)] struct Layer { neurons: Vec<Neuron>, } impl Layer { fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> { let mut outputs = Vec::new(); for neuron in &self.neurons { let output = neuron.propagate(inputs); outputs.push(output); } outputs } }
If we try to compile it, we get our first borrow-checker failure:
error[E0382]: use of moved value: `inputs`
--> src/lib.rs
|
| fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> {
| ------ move occurs because `inputs` has
| type `Vec<f32>`, which does not
| implement the `Copy` trait
...
| let output = neuron.propagate(inputs);
| ^^^^^^
| value moved here, in previous
| iteration of loop
Obviously, the compiler is right: after invoking
neuron.propagate(inputs), we lose ownership of
inputs, so we can't use it in the loop's consecutive
iterations.
Fortunately, the fix is easy and boils down to making
Neuron::propagate() work on borrowed values:
impl Layer { fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> { /* ... */ for neuron in &self.neurons { let output = neuron.propagate(&inputs); /* ... */ } /* ... */ } } /* ... */ impl Neuron { fn propagate(&self, inputs: &[f32]) -> f32 { /* ... */ } }
To reiterate, the code we have at the moment is:
impl Layer { fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> { let mut outputs = Vec::new(); for neuron in &self.neurons { let output = neuron.propagate(&inputs); outputs.push(output); } outputs } }
... and, would you believe it, this particular pattern is called mapping and the standard library also provides a method for it!
impl Layer { fn propagate(&self, inputs: Vec<f32>) -> Vec<f32> { self.neurons .iter() .map(|neuron| neuron.propagate(&inputs)) .collect() } }
Currently we've got nowhere else to go, but to complete
Neuron::propagate() - as before, let's start with a
crude,
superfund-ish
version:
impl Neuron { fn propagate(&self, inputs: &[f32]) -> f32 { let mut output = 0.0; for i in 0..inputs.len() { output += inputs[i] * self.weights[i]; } output += self.bias; if output > 0.0 { output } else { 0.0 } } }
This snippet contains two unidiomatic constructs and one potential bug - let's start with the latter.
Since we're iterating through self.weights using length
from inputs, we've got three edge cases:
-
When
inputs.len() < self.weights.len(), -
When
inputs.len() == self.weights.len(), -
When
inputs.len() > self.weights.len().
Our code lays on the assumption that #2 is always true, but it's a silent assumption: we don't enforce it anywhere! If we mistakenly passed less or more inputs, we'd get either an invalid result or a crash.
There are at least two ways we could go around improving it:
-
We could change
Neuron::propagate()to return an error message:impl Neuron { fn propagate(&self, inputs: &[f32]) -> Result<f32, String> { if inputs.len() != self.weights.len() { return Err(format!( "got {} inputs, but {} inputs were expected", inputs.len(), self.weights.len(), )); } /* ... */ } }
... or, using one of the crates I love the most - thiserror:
pub type Result<T> = std::result::Result<T, Error>; #[derive(Debug, Error)] pub enum Error { #[error("got {got} inputs, but {expected} inputs were expected")] MismatchedInputSize { got: usize, expected: usize, }, } /* ... */ impl Neuron { fn propagate(&self, inputs: &[f32]) -> Result<f32> { if inputs.len() != self.weights.len() { return Err(Error::MismatchedInputSize { got: inputs.len(), expected: self.weights.len(), }); } /* ... */ } }
-
We could use
assert_eq!()/panic!():impl Neuron { fn propagate(&self, inputs: &[f32]) -> f32 { assert_eq!(inputs.len(), self.weights.len()); /* ... */ } }
In most cases, the first variant is better, because it allows for the caller to catch the error and handle it easily - in our case though, the error reporting is simply not worth it, because:
-
If this assertion ever fails, it means that our implementation is most likely wrong and there's nothing users could do on their side to mitigate the issue.
-
This is a toy project, we've already got like fifty other ideas hanging in the air tonight, no need to waste our time.
So:
impl Neuron { fn propagate(&self, inputs: &[f32]) -> f32 { assert_eq!(inputs.len(), self.weights.len()); /* ... */ } }
As for the idioms - this one:
impl Neuron { fn propagate(&self, inputs: &[f32]) -> f32 { /* ... */ if output > 0.0 { output } else { 0.0 } } }
... is f32::max() in disguise:
impl Neuron { fn propagate(&self, inputs: &[f32]) -> f32 { /* ... */ output.max(0.0) } }
While this one:
impl Neuron { fn propagate(&self, inputs: &[f32]) -> f32 { /* ... */ let mut output = 0.0; for i in 0..inputs.len() { output += inputs[i] * self.weights[i]; } /* ... */ } }
... can be simplified first with .zip():
impl Neuron { fn propagate(&self, inputs: &[f32]) -> f32 { /* ... */ let mut output = 0.0; for (&input, &weight) in inputs.iter().zip(&self.weights) { output += input * weight; } /* ... */ } }
... and then using .map() + .sum():
impl Neuron { fn propagate(&self, inputs: &[f32]) -> f32 { /* ... */ let mut output = input .iter() .zip(&self.weights) .map(|(input, weight)| input * weight) .sum::<f32>(); /* ... */ } }
Voilà:
impl Neuron { fn propagate(&self, inputs: &[f32]) -> f32 { assert_eq!(inputs.len(), self.weights.len()); let output = inputs .iter() .zip(&self.weights) .map(|(input, weight)| input * weight) .sum::<f32>(); (self.bias + output).max(0.0) } }
It's unquestionably beautiful - but does it work? Can it recognize a cat? Can we use it to predict future Dogecoin prices?
Coding: new()
Up to this point we were focused so much on the algorithm that we gave little to no thought to contructors - but how could we ever play with a network we cannot create?
Our first approach for creating a constructor could be a plain, no-op function of:
#[derive(Debug)] pub struct Network { layers: Vec<Layer>, } impl Network { pub fn new(layers: Vec<Layer>) -> Self { Self { layers } } /* ... */ }
... but it won't do in this case, because - as we've already
established - we'd like to keep Layer and
Neuron outside the public interface.
If you recall our previous post, you might remember that we were talking a lot about random numbers - so if there's one thing I'm certain, it's that we'll need something in the lines of:
impl Network { pub fn random() -> Self { todo!() } }
In order to randomize a network, we'll need to know the number of its layers and number of neurons per each layer - they all can be described with a single vector:
impl Network { pub fn random(neurons_per_layer: Vec<usize>) -> Self { todo!() } }
... or, in a bit more elegant way:
#[derive(Debug)] pub struct LayerTopology { pub neurons: usize, } impl Network { pub fn random(layers: Vec<LayerTopology>) -> Self { todo!() } /* ... */ } // By the way, notice how creating a separate type allowed us to untangle // argument's name to just `layers`. // // Initially we went with `neurons_per_layer`, because `Vec<usize>` doesn't // provide enough information to tell what this `usize` represents - using a // separate type makes the intention explicit.
Now, if you look real close at a neural network's layer:
... perhaps you'll notice that it's actually defined by
two numbers: its input and output size - does it mean our
single-field LayerTopology is wrong? Au contraire!
What we've done is, as I like to call it, exploiting domain knowledge.
Inside a FFNN, all layers are connected consecutively, front-to-back:
... because layer A's output is layer B's input, if we went with:
#[derive(Debug)] pub struct LayerTopology { pub input_neurons: usize, pub output_neurons: usize, }
... then not only would we make our interface unwieldy, but - what's
more gruesome - we'd have to implement an additional validation
ensuring that
layer[0].output_neurons == layer[1].input_neurons etc.
are met - pure nonsense!
Noting this simple fact that consecutive layers must have matching inputs & outputs allows us to simplify the code before it's been even written.
As for the implementation, a crude approach would be:
impl Network { pub fn random(layers: Vec<LayerTopology>) -> Self { let mut built_layers = Vec::new(); for i in 0..(layers.len() - 1) { let input_size = layers[i].neurons; let output_size = layers[i + 1].neurons; built_layers.push(Layer::random( input_size, output_size, )); } Self { layers: built_layers } } }
... and now let's rustify it -- care to guess what happens when you
call
Network::random(vec![])?
impl Network { pub fn random(layers: Vec<LayerTopology>) -> Self { // Network with just one layer is technically doable, but doesn't // make much sense: assert!(layers.len() > 1); /* ... */ } }
There, better.
As for the for loop - iterating by adjacent items
is another pattern covered by the standard library, via a function
called .windows():
impl Network { pub fn random(layers: Vec<LayerTopology>) -> Self { /* ... */ for adjacent_layers in layers.windows(2) { let input_size = adjacent_layers[0].neurons; let output_size = adjacent_layers[1].neurons; /* ... */ } /* ... */ } }
In this case, switching to iterators is a no-brainer for me:
impl Network { pub fn random(layers: Vec<LayerTopology>) -> Self { let layers = layers .windows(2) .map(|layers| Layer::random(layers[0].neurons, layers[1].neurons)) .collect(); Self { layers } } }
And one final touch - when it doesn't make the code awkward, it's a good practice to accept borrowed values instead of owned:
impl Network { pub fn random(layers: &[LayerTopology]) -> Self { /* ... */ } }
More often than not, accepting borrowed values doesn't change much inside the function, but it makes it more versatile - i.e. with a borrowed array one can now do:
let network = Network::random(&[ LayerTopology { neurons: 8 }, LayerTopology { neurons: 15 }, LayerTopology { neurons: 2 }, ]);
... and:
let layers = vec![ LayerTopology { neurons: 8 }, LayerTopology { neurons: 15 }, LayerTopology { neurons: 2 }, ]; let network_a = Network::random(&layers); let network_b = Network::random(&layers); // ^ no need to .clone()
What's next, what's next... checks notes... ah,
Layer::random()!
impl Layer { fn random(input_size: usize, output_size: usize) -> Self { let mut neurons = Vec::new(); for _ in 0..output_size { neurons.push(Neuron::random(input_size)); } Self { neurons } } /* ... */ }
... or:
impl Layer { fn random(input_size: usize, output_size: usize) -> Self { let neurons = (0..output_size) .map(|_| Neuron::random(input_size)) .collect(); Self { neurons } } }
Finally, the last piece of our chain - Neuron::random():
impl Neuron { fn random(input_size: usize) -> Self { let bias = todo!(); let weights = (0..input_size) .map(|_| todo!()) .collect(); Self { bias, weights } } /* ... */ }
Contrary to C++ or Python, Rust's standard library doesn't provide any pseudorandom number generator - do you know what it means?
it's crates.io time!
Which crate should we choose? Well, let's see:
When it comes to PRNGs,
rand is the
de facto standard,
extremely versatile
crate which allows to generate not only pseudo-random numbers, but
also other types such as strings.
In order to fetch rand, we have to add it to our
Cargo.toml:
# ... [dependencies] rand = "0.8"
... and then:
use rand::Rng; /* ... */ impl Neuron { fn random(input_size: usize) -> Self { let mut rng = rand::thread_rng(); let bias = rng.gen_range(-1.0..=1.0); let weights = (0..input_size) .map(|_| rng.gen_range(-1.0..=1.0)) .collect(); Self { bias, weights } } }
Neat.
Certainly, rng.gen_range(-1.0..=1.0) predicts Dogecoin
prices quite accurately - but is there a way we could ensure our
entire
network works as intended?
Testing
A pure function is a function whose given the same arguments, always returns the same value - for instance, this is a pure function:
pub fn add(x: usize, y: usize) -> usize { x + y }
... while this one is not:
pub fn read(path: impl AsRef<Path>) -> String { std::fs::read_to_string(path).unwrap() }
(add(1, 2) will always return 3, while
read("file.txt") will return different strings depending
on what the file happens to contain at the moment.)
Pure functions are nice, because they can be tested in isolation:
// This test always succeeds // (i.e it is *deterministic*) #[test] fn test_add() { assert_eq!(add(1, 2), 3); } // This test might succeed or it might fail, impossible to anticipate // (i.e. it is *indeterministic*) #[test] fn test_read() { assert_eq!( std::fs::read_to_string("serials-to-watch.txt"), "killing eve", ); }
Unfortunately, the way we generate numbers inside
Neuron::random() makes it impure, which can be
easily proven with:
#[test] fn random_is_pure() { let neuron_a = Neuron::random(4); let neuron_b = Neuron::random(4); // If `Neuron::random()` was pure, then both neurons would always have // to be the same: assert_eq!(neuron_a, neuron_b); }
Testing unpure functions is hard, because there's not much we can assert reliably:
/* ... */ #[cfg(test)] mod tests { use super::*; #[test] fn random() { let neuron = Neuron::random(4); assert!(/* what? */); } }
We might try:
#[test] fn test() { let neuron = Neuron::random(4); assert_eq!(neuron.weights.len(), 4); }
... but that's a useless test, it doesn't actually prove anything.
On the other hand, making Neuron::random() a pure
function seems... preposterous? What's the point of randomizing, if
the outcome would always remain the same?
The way I usually reconcile both worlds is by looking at the source of impurity - in this case, it is:
impl Neuron { fn random(input_size: usize) -> Self { let mut rng = rand::thread_rng(); // whoopsie /* ... */ } }
If instead of invoking thread_rng(), we accepted a
parameter with the randomizer:
use rand::{Rng, RngCore}; /* ... */ impl Network { pub fn random(rng: &mut dyn RngCore, layers: &[LayerTopology]) -> Self { let layers = layers .windows(2) .map(|layers| Layer::random(rng, layers[0].neurons, layers[1].neurons)) .collect(); /* ... */ } /* ... */ } /* ... */ impl Layer { fn random(rng: &mut dyn RngCore, input_size: usize, output_size: usize) -> Self { let neurons = (0..output_size) .map(|_| Neuron::random(rng, input_size)) .collect(); /* ... */ } /* ... */ } /* ... */ impl Neuron { fn random(rng: &mut dyn RngCore, input_size: usize) -> Self { /* ... */ } /* ... */ }
... then we could use a fake, predictable PRNG in our tests, while users would simply pass an actual PRNG of their choosing.
Because the rand crate doesn't provide a predictable or
seedable PRNG, we have to make use of another crate - I like
rand_chacha
(easy to remember, you've probably already memorized it):
# ... [dependencies] rand = "0.8" [dev-dependencies] rand_chacha = "0.3"
... which allows us to do:
#[cfg(test)] mod tests { use super::*; use rand::SeedableRng; use rand_chacha::ChaCha8Rng; #[test] fn random() { // Because we always use the same seed, our `rng` in here will // always return the same set of values let mut rng = ChaCha8Rng::from_seed(Default::default()); let neuron = Neuron::random(&mut rng, 4); assert_eq!(neuron.bias, /* ... */); assert_eq!(neuron.weights, &[/* ... */]); } }
We don't know which numbers will be returned just yet, but finding out is easy - we'll just start with zeros and then copy-paste numbers from the test's output:
#[test] fn random() { /* ... */ assert_eq!(neuron.bias, 0.0); assert_eq!(neuron.weights, &[0.0, 0.0, 0.0, 0.0]); }
First cargo test gives us:
thread '...' panicked at 'assertion failed: `(left == right)` left: `-0.6255188`, right: `0.0`
... so:
#[test] fn random() { /* ... */ assert_eq!(neuron.bias, -0.6255188); /* ... */ }
Another cargo test:
thread '...' panicked at 'assertion failed: `(left == right)` left: `[0.67383957, 0.8181262, 0.26284897, 0.5238807]`, right: `[0.0, 0.0, 0.0, 0.0]`', src/lib.rs:29:5
... and we end up with:
#[test] fn random() { /* ... */ assert_eq!( neuron.weights, &[0.67383957, 0.8181262, 0.26284897, 0.5238807] ); }
Notice the numbers are different and that's alright - they are
allowed to be different as long as each
cargo test consistently works on the same set of numbers
(and it does, because we used a PRNG with a constant seed).
Before moving on, there's one more topic we have to cover here: floating-point inaccuracies.
The type we're using, f32, models a 32-bit floating-point
number that can represent values between ~1.2*10^-38 and
~3.4*10^38 - alas, it cannot represent all of those
numbers, just some.
For instance, with f32 you cannot encode exactly
0.15 - it'll always be off by a bit:
fn main() { println!("{:.10}", 0.15f32); // prints: 0.1500000060 }
... same with, say, 0.45:
fn main() { println!("{:.10}", 0.45f32); // prints: 0.4499999881 }
Usually it doesn't matter, because floating-point numbers were never made to be exact (only fast) - but when it does come up, it hits one like a brick falling from the sky:
#[test] fn test() { assert_eq!(0.45f32, 0.15 + 0.15 + 0.15); }
thread 'test' panicked at 'assertion failed: `(left == right)` left: `0.45`, right: `0.45000002`'
To avoid reinventing the wheel, I'll just drop this link: What Every Programmer Should Know About Floating-Point Arithmetic - if you haven't read about floating-point numbers yet, I encourage you to give it a shot!
So, if we shouldn't compare numbers exactly, what can we do? Compare them approximately!
#[test] fn test() { let actual: f32 = 0.1 + 0.2; let expected = 0.3; assert!((actual - expected).abs() < f32::EPSILON); }
This is the standard way to compare floats across all programming languages that implement IEEE 754 (so, like, all programming languages) - instead of fishing for an exact result, you compare both numbers with a margin of error (also called tolerance).
Because comparing numbers this way is awkward, it's more cushy to either do it via a macro:
macro_rules! assert_almost_eq { ($left:expr, $right:expr) => { let left: f32 = $left; let right: f32 = $right; assert!((left - right).abs() < f32::EPSILON); } } #[test] fn test() { assert_almost_eq!(0.45f32, 0.15 + 0.15 + 0.15); }
... or - which is the best approach - using a crate such as approx:
#[test] fn test() { approx::assert_relative_eq!(0.45f32, 0.15 + 0.15 + 0.15); }
I personally like approx, so let's add it to our neural
network's Cargo.toml:
# ... [dev-dependencies] approx = "0.4" rand_chacha = "0.3"
... and then adjust the tests:
use super::*; use approx::assert_relative_eq; use rand::SeedableRng; use rand_chacha::ChaCha8Rng; #[test] fn random() { let mut rng = ChaCha8Rng::from_seed(Default::default()); let neuron = Neuron::random(&mut rng, 4); assert_relative_eq!(neuron.bias, -0.6255188); assert_relative_eq!( neuron.weights.as_slice(), [0.67383957, 0.8181262, 0.26284897, 0.5238807].as_ref() ); }
This covers half of neuron's functions - thankfully, knowing what we
know now, writing a test for Neuron::propagate() will go
easy:
#[cfg(test)] mod tests { /* ... */ #[test] fn random() { /* ... */ } #[test] fn propagate() { todo!() } }
How can we ensure propagate() works correctly? By
computing the expected response manually:
#[test] fn propagate() { let neuron = Neuron { bias: 0.5, weights: vec![-0.3, 0.8], }; // Ensures `.max()` (our ReLU) works: assert_relative_eq!( neuron.propagate(&[-10.0, -10.0]), 0.0, ); // `0.5` and `1.0` chosen by a fair dice roll: assert_relative_eq!( neuron.propagate(&[0.5, 1.0]), (-0.3 * 0.5) + (0.8 * 1.0) + 0.5, ); // We could've written `1.15` right away, but showing the entire // formula makes our intentions clearer }
From this point, implementing tests for Layer and
Network gets pretty straightforward and thus has been
left as an exercise for the reader :-)
Closing thoughts
What have we created, exactly?
It might seem that what we've implemented has nothing to do with learning or simulating:
-
what about the eyes?
-
where's the code responsible for movement?
-
how did you create that greenish, Fallout-style terminal?
... but that's only because the neural network itself, while being a relatively complex piece of our codebase, doesn't do much on its own - thou shall not worry, though, for in the end all the pieces shall fit together.
In the meantime, feel free to checkout the source code.
Is our design inflated?
When you search for python neural network from scratch,
you'll find lots of articles which encapsulate FFNNs in a few lines of
Python code - compared to them, our design seems inflated, why is that
so?
It's because we could learn more this way - we could've coded our network in 1/10th of its current size by using nalgebra, we could've used one of the already-existing crates, but it's not the destination that matters, it's the journey.
What’s next?
At the moment we've got a bare-bones FFNN at hand - in the next article we'll be implementing the genetic algoritm and we'll be connecting it to our neural network. The last post will be all about WebAssembly-ing our crates together to end up with our opus magnum: flying birds.