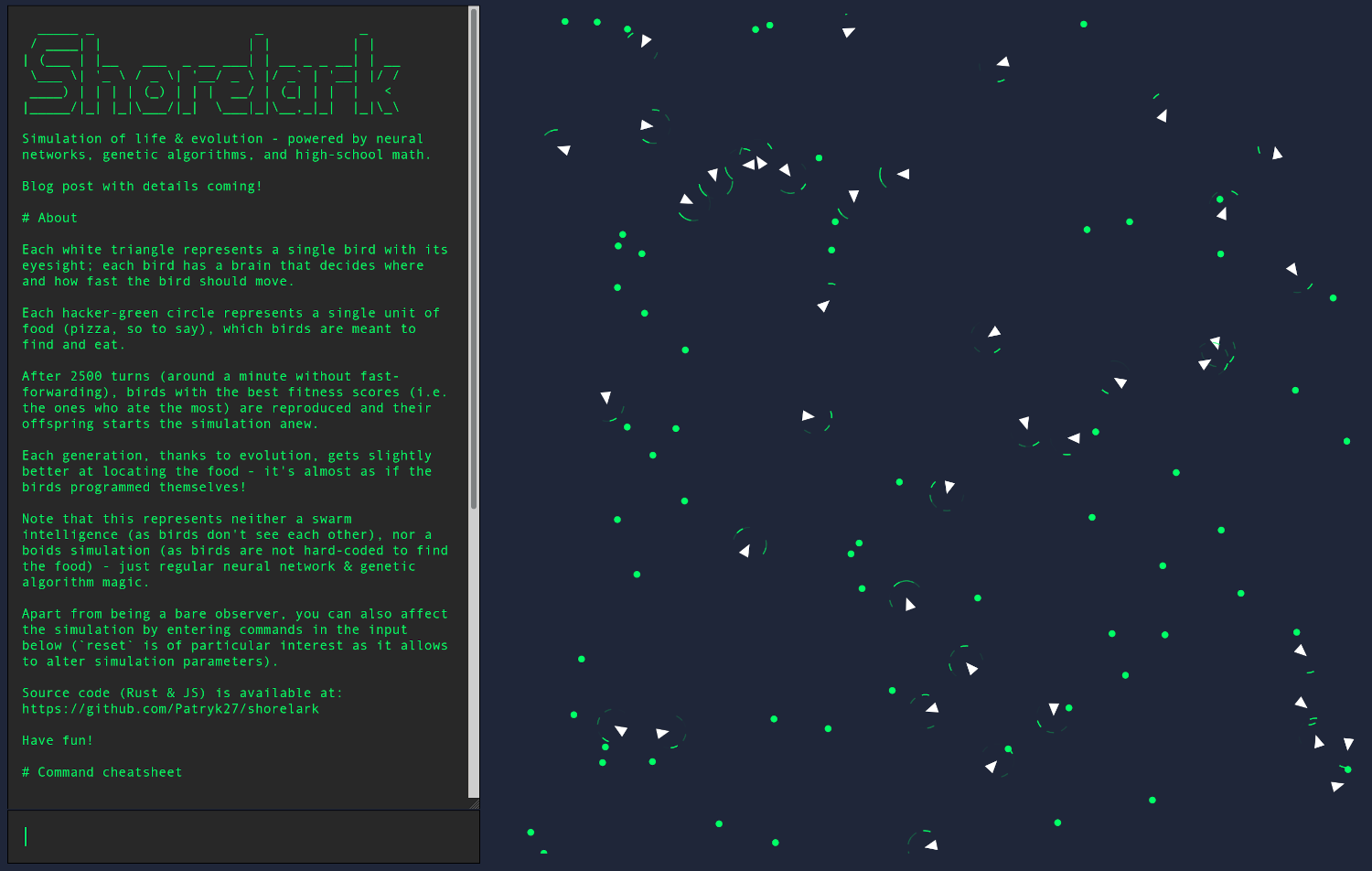
Learning to Fly: Let's simulate evolution in Rust (pt 3)

This is the third part of the Learning to Fly series in which we're coding a simulation of evolution using neural network and genetic algorithm:

In the previous post we implemented a simple feed-forward neural network that could propagate numbers through its randomized layers - it was the first milestone in our effors to create a functioning brain.

Randomness can get us only so far, though - for the most part, evolution is about making small, incremental changes so that the system gets better over time -- so that our brains begin to accumulate knowledge and function as we expect them (just catch the food, birdies!).

But how can we train a bunch of floating-point numbers?

Plan

Today we'll learn how a genetic algorithm works by implementing one in Rust. We'll examine in-depth how selection, crossover and mutation all come together and allow for the computer to find complex solutions seemingly out of thin air.

We'll try to remain generic, meaning that instead of hard-coding a particular selection or crossover algorithm, we'll use traits to create a library that could be even published to crates.io!

As in the previous part, so we'll investigate various intricacies of Rust's syntax today, focusing a lot on the terminology.

Hopefully, by the end of this post you'll be able to say: I could've implemented all this on my own!

Introduction

First, let's recap how a genetic algorithm works and what's the point of this venture.

Our problem is that we've got an object - a neural network - that's defined by a whole lot of parameters. There are so many of them that, even for the smallest of networks, we couldn't possibly brute-force all of their combinations in our lifetime.

What we can do is to kinda mimic the nature: if we started with a bunch of random suboptimal solutions, we could try improving them to get - over time - gradually better answers.

One of the methods that allows to simulate all this evolutionary machinery is the eponymous genetic algorithm - it starts with a bunch of random solution-candidates (a population), which are then improved using mutation and crossover, utilizing a fitness function to evaluate solutions (individuals) found so far:

Vegetable manufacturers don't want you to know this, but there exists a straightforward procedure to becoming a carrot tycoon that's based on a enetic algorithm:

10  go to your garden
20  sow a few random carrots
30  wait for those carrots to sprout
40  choose the best carrot-children and sow them
50  goto 30

in this world:
- population = carrots
- individual = carrot
- mutation & crossover = happen automatically (free labor!)
- fitness function = your eyes & brain

By now, most of those words ought to sound familiar to you - we've already gone through the basics of evolutionary computation in the first article; by the end of this article, you'll have answered questions such as:

• but how do you choose the individuals? there must be like a thousand ways to do it!
  (psst: oh my yes, there are)

• but how do you represent their genomes? there must be like a thousand ways to do it!
  (psst: oh my yes, there are)

• but how do you implement it in Rust? you promised it'll work inside a web browser!
  (psst: oh my yes, it will)

Coding: Outline

We'll start by creating a second crate inside our workspace:

$ cd shorelark/libs
$ cargo new genetic-algorithm --name lib-genetic-algorithm --lib

That's some nice lib.rs Cargo created for us - let's replace it with an entry point:

pub struct GeneticAlgorithm;

Our genetic algorithm will provide only one functionality - sometimes it's called iterate, sometimes it's called step or process - I've tossed a coin and decided on:

impl GeneticAlgorithm {
    pub fn evolve(&self) {
        todo!()
    }
}

What are we evolving? A population, of course!

impl GeneticAlgorithm {
    pub fn evolve(&self, population: &[???]) -> Vec<???> {
        todo!()
    }
}

Our actual problem will depend on neural networks, but since we want for this library to be generic, we can't force it to accept a hard-coded NeuralNetwork - instead, we can introduce a type parameter:

impl GeneticAlgorithm {
    pub fn evolve<I>(&self, population: &[I]) -> Vec<I> {
        todo!()
    }
}

Learning from past mistakes, let's not forget about preconditions:

impl GeneticAlgorithm {
    pub fn evolve<I>(&self, population: &[I]) -> Vec<I> {
        assert!(!population.is_empty());

        /* ... */
    }
}

As for the algorithm itself - the outline is:

impl GeneticAlgorithm {
    pub fn evolve<I>(&self, population: &[I]) -> Vec<I> {
        /* ... */

        (0..population.len())
            .map(|_| {
                // TODO selection
                // TODO crossover
                // TODO mutation
                todo!()
            })
            .collect()
    }
}

Coding: Selection

At this point, inside the loop, we have to pick two individuals - they will become parents and "create" a digital offspring for us.

Choosing individuals is called the selection stage of a genetic algorithm and it should satisfy the following two properties:

• each individual should have a non-zero chance of being picked,

• an individual with a higher fitness score should get picked, on average, more often than an individual with a lower fitness score.

Because we have to calculate fitness scores, let's start by thinking how we want users to provide their fitness function - as trivial as it sounds, there are at least two exclusive approaches here:

1. Fitness function as a parameter of an individual:

   libs/genetic-algorithm/src/lib.rs

   impl GeneticAlgorithm {
       pub fn evolve<I>(
           &self,
           population: &[I],
           evaluate_fitness: &dyn Fn(&I) -> f32,
       ) -> Vec<I> {
           /* ... */
       }
   }
   

2. Fitness score as a property of an individual:

   libs/genetic-algorithm/src/lib.rs

   pub trait Individual {
       fn fitness(&self) -> f32;
   }
   
   impl GeneticAlgorithm {
       pub fn evolve<I>(&self, population: &[I]) -> Vec<I>
       where
           I: Individual,
       {
           /* ... */
       }
   }
   

First approach:

• ✅ allows to provide many different fitness functions for one kind of an individual, which might prove to be useful for somebody (not us, though),

• ❌ requires specifying fitness function for each invocation of .evolve(), which feels a bit awkward.

Second approach:

• ✅ allows to encapsulate all the individual-oriented attributes into a single trait, making it easy for users to discover what they need to provide,

• ❌ specifying different fitness functions is possible, but a bit more tricky.

My guts vote 213:7 for introducing a trait (a trait that, as you'll see later, we would need anyway), so a trait it is.

As for the selection method, we'll use an algorithm called fitness proportionate selection (also known as roulette wheel selection), because it's easy to reason about - to understand how it works, let's imagine we've got the following three individuals:

If we placed them all on a roulette wheel - or a pie chart, for all it matters - with each individual getting a slice of wheel as large as proportion of their fitness score to the entire population:

... then randomizing an individual would boil down to "spinning" the wheel with random amount of force and seeing what comes up:

Living up to the genericness promise, instead of hard-coding our library to use roulette wheel selection, let's create a trait - this way users will be able to provide any algorithm they fancy:

pub trait SelectionMethod {
    fn select(&self);
}

A selection method has to have access to the entire population:

pub trait SelectionMethod {
    fn select<I>(&self, population: &[I]) -> &I
    where
        I: Individual;
}

... and, for clarity, let's annotate the lifetime:

pub trait SelectionMethod {
    fn select<'a, I>(&self, population: &'a [I]) -> &'a I
    where
        I: Individual;
}

We're going to need random numbers any minute now, so:

# ...

[dependencies]
rand = "0.8"

[dev-dependencies]
rand_chacha = "0.3"

Learning from our past troubles with thread_rng(), let's pass the PRNG via a parameter:

use rand::RngCore;

/* ... */

pub trait SelectionMethod {
    fn select<'a, I>(&self, rng: &mut dyn RngCore, population: &'a [I]) -> &'a I
    where
        I: Individual;
}

Ain't that a beautiful signature?

As for the implementation:

pub struct RouletteWheelSelection;

impl SelectionMethod for RouletteWheelSelection {
    fn select<'a, I>(&self, rng: &mut dyn RngCore, population: &'a [I]) -> &'a I
    where
        I: Individual,
    {
        todo!()
    }
}

... we could do it by hand:

impl SelectionMethod for RouletteWheelSelection {
    fn select<'a, I>(&self, rng: &mut dyn RngCore, population: &'a [I]) -> &'a I
    where
        I: Individual,
    {
        let total_fitness: f32 = population
            .iter()
            .map(|individual| individual.fitness())
            .sum();

        // This is a naïve approach for demonstration purposes - a more
        // efficient implementation would invoke `rng` just once
        loop {
            let indiv = population
                .choose(rng)
                .expect("got an empty population");

            let indiv_share = indiv.fitness() / total_fitness;

            if rng.gen_bool(indiv_share as f64) {
                return indiv;
            }
        }
    }
}

... but a code par excellence would be <drums /> no code at all!

If you go through the rand's documentation, you might just spot a trait called SliceRandom - if you take a look inside it, you might just spot a method called choose_weighted() that happens to be doing exactly the exact thing we need:

use rand::seq::SliceRandom;
use rand::{Rng, RngCore};

/* ... */

impl SelectionMethod for RouletteWheelSelection {
    fn select<'a, I>(&self, rng: &mut dyn RngCore, population: &'a [I]) -> &'a I
    where
        I: Individual,
    {
        population
            .choose_weighted(rng, |individual| individual.fitness())
            .expect("got an empty population")
    }
}

(thanks to @javiertury for pointing out that this method exists.)

Apart from trusting rand developers, how can we be sure choose_weighted() does the thing we need? By testing it!

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn roulette_wheel_selection() {
        todo!();
    }
}

Path to the TDD-nirvana is strawn with roses and we're about to get bit by one of their thorns:

#[cfg(test)]
mod tests {
    use super::*;
    use rand::SeedableRng;
    use rand_chacha::ChaCha8Rng;

    #[test]
    fn roulette_wheel_selection() {
        let mut rng = ChaCha8Rng::from_seed(Default::default());

        let population = vec![ /* what here? */ ];
        let actual = RouletteWheelSelection::new().select(&mut rng, &population);

        assert!(/* what here? */);
    }
}

At this point we've got two problems:

1. Since Individual is a trait, how can we fake it for testing purposes?

2. Since .select() returns just a single individual, how can we be sure it's random?

Starting from the top: creating fake objects for testing purposes is called mocking - and while there are mocking solutions for Rust, I gotta admit I've never been a fan of the concept of a mock, as best presented in a song:

Friend, either you're closing your eyes
To a situation you do not wish to acknowledge
Or you are not aware of the caliber of disaster indicated
By the presence of mocks in your repository

[...]

Oh yes we got trouble, trouble, trouble!
With a "T"! Gotta rhyme it with "M"!
And that stands for Mock

My suggestion - one that doesn't require any external crates - it to create a dedicated testing-struct:

#[cfg(test)]
mod tests {
    /* ... */

    #[derive(Clone, Debug)]
    struct TestIndividual {
        fitness: f32,
    }

    impl TestIndividual {
        fn new(fitness: f32) -> Self {
            Self { fitness }
        }
    }

    impl Individual for TestIndividual {
        fn fitness(&self) -> f32 {
            self.fitness
        }
    }

    /* ... */
}

... which we can then use as:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn roulette_wheel_selection() {
        /* ... */

        let population = vec![
            TestIndividual::new(2.0),
            TestIndividual::new(1.0),
            TestIndividual::new(4.0),
            TestIndividual::new(3.0),
        ];

        /* ... */
    }
}

What about the assertion, though? A test such as this one:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn roulette_wheel_selection() {
        /* ... */

        let actual = RouletteWheelSelection::new()
            .select(&mut rng, &population);

        assert!(actual, &population[2]);
    }
}

... doesn't inspire confidence, because it doesn't prove that the fitness scores are actually being considered - a totally invalid implementation such as:

impl SelectionMethod for RouletteWheelSelection {
    fn select<'a, I>(/* ... */) -> &'a I
    where
        I: Individual,
    {
        &population[2]
    }
}

... would pass such test with flying colors!

Fortunately, we are not doomed - since we want to assess probability, instead of calling .select() just once, we can do it many times and look at the histogram:

#[cfg(test)]
mod tests {
    /* ... */
    use std::collections::BTreeMap;
    use std::iter::FromIterator;

    #[test]
    fn roulette_wheel_selection() {
        let mut rng = ChaCha8Rng::from_seed(Default::default());

        let population = vec![
            /* ... */
        ];

        let mut actual_histogram = BTreeMap::new();

        //          /--| nothing special about this thousand;
        //          v  | a number as low as fifty might do the trick, too
        for _ in 0..1000 {
            let fitness = RouletteWheelSelection
                .select(&mut rng, &population)
                .fitness() as i32;

            *actual_histogram
                .entry(fitness)
                .or_insert(0) += 1;
        }

        let expected_histogram = BTreeMap::from_iter([
            // (fitness, how many times this fitness has been chosen)
            (1, 0),
            (2, 0),
            (3, 0),
            (4, 0),
        ]);

        assert_eq!(actual_histogram, expected_histogram);
    }
}

cargo test (or cargo test --workspace, if you're in the virtual manifest's directory) returns:

thread '...' panicked at 'assertion failed: `(left == right)`
  left: `{1: 98, 2: 202, 3: 278, 4: 422}`,
 right: `{1: 0, 2: 0, 3: 0, 4: 0}`'

... proving that choose_weighted() works as advertised (higher fitness scores were chosen more frequently), so let's adjust the test:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn roulette_wheel_selection() {
        /* ... */

        let expected_histogram = BTreeMap::from_iter(vec![
            // (fitness, how many times this fitness has been chosen)
            (1, 98),
            (2, 202),
            (3, 278),
            (4, 422),
        ]);

        /* ... */
    }
}

Voilà - we've tested the untestable! Having the selection ready, let's recap where we've stopped:

impl GeneticAlgorithm {
    pub fn evolve<I>(&self, population: &[I]) -> Vec<I>
    where
        I: Individual,
    {
        /* ... */

        (0..population.len())
            .map(|_| {
                // TODO selection
                // TODO crossover
                // TODO mutation
                todo!()
            })
            .collect()
    }
}

What we have to figure out now is how to pass SelectionMethod in there - I see two approaches:

1. Using a parameter:

   impl GeneticAlgorithm {
       pub fn evolve<I, S>(
           &self,
           population: &[I],
           selection_method: &S,
       ) -> Vec<I>
       where
           I: Individual,
           S: SelectionMethod,
       {
           /* ... */
       }
   }
   

2. Using a constructor:

   libs/genetic-algorithm/src/lib.rs

   pub struct GeneticAlgorithm<S> {
       selection_method: S,
   }
   
   impl<S> GeneticAlgorithm<S>
   where
       S: SelectionMethod,
   {
       pub fn new(selection_method: S) -> Self {
           Self { selection_method }
       }
   
       pub fn evolve<I, S>(&self, population: &[I]) -> Vec<I>
       where
           I: Individual,
       {
           /* ... */
       }
   }
   

Facing this kind of decision, I think how often users will need to change that object:

A population is usually different each time one calls .evolve(), so it's convenient to accept it via parameter - on the other hand, the selection algorithm usually remains the same for the entire simulation, so it'll be more convenient for the users to provide it through the constructor.

Now we're almost ready to invoke the selection method:

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    /* ... */

    pub fn evolve<I>(&self, population: &[I]) -> Vec<I>
    where
        I: Individual,
    {
        /* ... */

        (0..population.len())
            .map(|_| {
                let parent_a = self.selection_method.select(rng, population);
                let parent_b = self.selection_method.select(rng, population);

                // TODO crossover
                // TODO mutation
                todo!()
            })
            .collect()
    }
}

... the only thing we're missing is the PRNG:

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    /* ... */

    pub fn evolve<I>(&self, rng: &mut dyn RngCore, population: &[I]) -> Vec<I>
    where
        I: Individual,
    {
        /* ... */
    }
}

Coding: Crossover

Now that we have chosen two parent-individuals, it's time for the crossover phase.

Crossover (also known as recombination) takes two individuals and mixes them, creating a new~ish solution in result:

As compared to simply creating brand-new random individuals, crossover is neat in the sense that it tries to preserve knowledge - the idea is that mixing two good solutions will usually yield a solution that's both new and at least as good as the two solutions we already have - this allows to explore the search space without the risk of losing the best solutions discovered so far.

As in real world, crossover doesn't actually happen on individuals, but rather on their chromosomes - which is a fancy word for "the encoding of a solution":

A chromosome (also called genotype, though I'm convinced a biologist dies each time someone mixes both terms) is usually built from genes, and its structure depends on the underlying problem - sometimes it's convenient to model a chromosome as a bitset:

... sometimes it's more convenient to have a string:

... and we'll use what we already have - bunch of f32s representing weights of the neural network:

#[derive(Clone, Debug)]
pub struct Chromosome {
    genes: Vec<f32>,
}

Instead of exposing genes directly (via pub genes: ...​), we'll provide a handful of functions allowing to peek inside the chromosome - that's called encapsulation:

impl Chromosome {
    pub fn len(&self) -> usize {
        self.genes.len()
    }

    pub fn iter(&self) -> impl Iterator<Item = &f32> {
        self.genes.iter()
    }

    pub fn iter_mut(&mut self) -> impl Iterator<Item = &mut f32> {
        self.genes.iter_mut()
    }
}

Seizing the day, let's catch up on some cool traits from the standard library:

1. There's Index, which allows you to use the indexing operator - [] - on your type:

   use std::ops::Index;
   
   /* ... */
   
   // ---
   // | this is the type of expression you expect inside the square brackets
   // |
   // | e.g. if you implemented `Index<&str>`, you could write:
   // |   chromosome["yass"]
   // ------- v---v
   impl Index<usize> for Chromosome {
       type Output = f32;
   
       fn index(&self, index: usize) -> &Self::Output {
           &self.genes[index]
       }
   }
   

2. There's FromIterator, which allows you to .collect() into your type:

   // ---
   // | this is the type of the item an iterator should provide in order to be compatible
   // | with our chromosome
   // |
   // | (sometimes it's called the type an iterator *yields*)
   // |
   // | intuitively, since our chromosome is built of of floating-point numbers, we
   // | expect floating-point numbers in here as well
   // -------------- v-v
   impl FromIterator<f32> for Chromosome {
       fn from_iter<T: IntoIterator<Item = f32>>(iter: T) -> Self {
           Self {
               genes: iter.into_iter().collect(),
           }
       }
   }
   

3. Finally, there's IntoIterator, which works in the opposite way - it converts a type into an iterator:

   impl IntoIterator for Chromosome {
       type Item = f32;
       type IntoIter = std::vec::IntoIter<f32>;
   
       fn into_iter(self) -> Self::IntoIter {
           self.genes.into_iter()
       }
   }
   

As I said a few minutes ago:

[...] crossover doesn't actually happen on individuals, but rather on their chromosomes [...]

... which brings us to:

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    /* ... */

    pub fn evolve<I>(/* ... */) -> Vec<I>
    where
        I: Individual,
    {
        (0..population.len())
            .map(|_| {
                let parent_a = self.selection_method.select(rng, population).chromosome();
                let parent_b = self.selection_method.select(rng, population).chromosome();

                /* ... */
            })
            .collect()
    }
}

/* ... */

pub trait Individual {
    fn fitness(&self) -> f32;
    fn chromosome(&self) -> &Chromosome;
}

/* ... */

#[cfg(test)]
mod tests {
    /* ... */

    impl Individual for TestIndividual {
        fn fitness(&self) -> f32 {
            self.fitness
        }

        fn chromosome(&self) -> &Chromosome {
            panic!("not supported for TestIndividual")
        }
    }

    /* ... */
}

As for the crossover itself, there are many algorithms we could implement - usually it's best to try a few of them and see whichever plays best with given problem, but for simplicity, we'll go with uniform crossover, which can be described with a single drawing:

Same as before, let's start with a trait:

pub trait CrossoverMethod {
    fn crossover(
        &self,
        rng: &mut dyn RngCore,
        parent_a: &Chromosome,
        parent_b: &Chromosome,
    ) -> Chromosome;
}

... and a rudimentary implementation:

#[derive(Clone, Debug)]
pub struct UniformCrossover;

impl CrossoverMethod for UniformCrossover {
    fn crossover(
        &self,
        rng: &mut dyn RngCore,
        parent_a: &Chromosome,
        parent_b: &Chromosome,
    ) -> Chromosome {
        let mut child = Vec::new();
        let gene_count = parent_a.len();

        for gene_idx in 0..gene_count {
            let gene = if rng.gen_bool(0.5) {
                parent_a[gene_idx]
            } else {
                parent_b[gene_idx]
            };

            child.push(gene);
        }

        child.into_iter().collect()
    }
}

Your internal critic might've noticed a few things off about this code - rightfully so!

First, let's add an assertion:

impl CrossoverMethod for UniformCrossover {
    fn crossover(/* ... */) -> Chromosome {
        assert_eq!(parent_a.len(), parent_b.len());

        /* ... */
    }
}

Second, let's use a combinator - we already know this one from the previous post, it's .zip():

impl CrossoverMethod for UniformCrossover {
    fn crossover(/* ... */) -> Chromosome {
        assert_eq!(parent_a.len(), parent_b.len());

        parent_a
            .iter()
            .zip(parent_b.iter())
            .map(|(&a, &b)| if rng.gen_bool(0.5) { a } else { b })
            .collect()
    }
}

How neat!

Notice how by implementing .iter() and FromIterator a moment ago, we were able to reduce code in here to a bare minimum that conveys the essence of the uniform crossover.

Your internal critic might still be alerted that something's missing...​ hmm...​ ah, tests!

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn uniform_crossover() {
        let mut rng = ChaCha8Rng::from_seed(Default::default());
        let parent_a = todo!();
        let parent_b = todo!();
        let child = UniformCrossover.crossover(&mut rng, &parent_a, &parent_b);

        assert!(/* ... */);
    }
}

What we want to verify, in plain words, is that child is 50% parent_a + 50% parent_b.

My suggestion is to generate two distinct chromosomes (they don't have to be random, just build out of different genes):

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn uniform_crossover() {
        /* ... */

        let parent_a: Chromosome = (1..=100).map(|n| n as f32).collect();
        let parent_b: Chromosome = (1..=100).map(|n| -n as f32).collect();

        // First parent will be:
        //   [1, 2, /* ... */, 100]
        //
        // Second parent will look similar, but with reversed signs:
        //   [-1, -2, /* ... */, -100]
        //
        // Just like in the histogram, the concrete number of genes doesn't
        // matter - 100 will nicely round up to 100%, that's all

        /* ... */
    }
}

... and then compare how much child differs from each of them:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn uniform_crossover() {
        /* ... */

        let child = UniformCrossover.crossover(&mut rng, &parent_a, &parent_b);

        // Number of genes different between `child` and `parent_a`
        let diff_a = child.iter().zip(parent_a).filter(|(c, p)| *c != p).count();

        // Number of genes different between `child` and `parent_b`
        let diff_b = child.iter().zip(parent_b).filter(|(c, p)| *c != p).count();

        assert_eq!(diff_a, 0);
        assert_eq!(diff_b, 0);
    }
}

cargo test says:

thread '...' panicked at 'assertion failed: `(left == right)`
  left: `49`,
 right: `0`'

... so let's adjust the test:

assert_eq!(diff_a, 49);

Another cargo test will fail on the second assertion:

thread '...' panicked at 'assertion failed: `(left == right)`
  left: `51`,
 right: `0`'

... so:

assert_eq!(diff_b, 51);

To recall, what we've got is:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn uniform_crossover() {
        /* ... */

        assert_eq!(diff_a, 49);
        assert_eq!(diff_b, 51);
    }
}

... meaning that our child got 49% of its genome from parent_a and 51% from parent_b - this ultimately proves our uniform crossover picks genes from both parents at equal probability.

(we didn't get an exact 50% - 50% match, but that's just probability being probability.)

Now we can pass CrossoverMethod next to SelectionMethod:

pub struct GeneticAlgorithm<S> {
    selection_method: S,
    crossover_method: Box<dyn CrossoverMethod>,
}

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    pub fn new(
        selection_method: S,
        crossover_method: impl CrossoverMethod + 'static,
    ) -> Self {
        Self {
            selection_method,
            crossover_method: Box::new(crossover_method),
        }
    }

    /* ... */
}

... and then we can call it:

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    /* ... */

    pub fn evolve<I>(&self, rng: &mut dyn RngCore, population: &[I]) -> Vec<I>
    where
        I: Individual,
    {
        /* ... */

        (0..population.len())
            .map(|_| {
                /* ... */

                let mut child = self.crossover_method.crossover(rng, parent_a, parent_b);

                /* ... */
            })
            .collect()
    }
}

Coding: Mutation

Now that we have a semi-new chromosome at hand, it's time to introduce some diversity!

Mutation, next to crossover and selection, is the third genetic operator - it takes a chromosome and introduces one or many random changes to it:

As in The Actual Evolution®, the role of mutation is to explore solutions that were not present in the initial population; it also prevents the algoritm from getting stuck in a local optimum, as it keeps the population changed from one generation to another.

Since we already have Chromosome implemented, mutation's going to be smooth as butter:

pub trait MutationMethod {
    fn mutate(&self, rng: &mut dyn RngCore, child: &mut Chromosome);
}

We'll use Gaussian mutation, which is a fancy way of saying "we'll add or subtract random numbers from the genome". Contrary to our parameter-less selection method, Gaussian mutation requires specifying two arguments:

#[derive(Clone, Debug)]
pub struct GaussianMutation {
    /// Probability of changing a gene:
    /// - 0.0 = no genes will be touched
    /// - 1.0 = all genes will be touched
    chance: f32,

    /// Magnitude of that change:
    /// - 0.0 = touched genes will not be modified
    /// - 3.0 = touched genes will be += or -= by at most 3.0
    coeff: f32,
}

impl GaussianMutation {
    pub fn new(chance: f32, coeff: f32) -> Self {
        assert!(chance >= 0.0 && chance <= 1.0);

        Self { chance, coeff }
    }
}

impl MutationMethod for GaussianMutation {
    fn mutate(&self, rng: &mut dyn RngCore, child: &mut Chromosome) {
        for gene in child.iter_mut() {
            let sign = if rng.gen_bool(0.5) { -1.0 } else { 1.0 };

            if rng.gen_bool(self.chance as f64) {
                *gene += sign * self.coeff * rng.gen::<f32>();
            }
        }
    }
}

As for the tests, instead of doing fn test() like before, this time I'd like to show you a bit different approach - let's talk edge cases:

#[cfg(test)]
mod tests {
    /* ... */

    mod gaussian_mutation {
        mod given_zero_chance {
            mod and_zero_coefficient {
                #[test]
                fn does_not_change_the_original_chromosome() {
                    todo!();
                }
            }

            mod and_nonzero_coefficient {
                #[test]
                fn does_not_change_the_original_chromosome() {
                    todo!();
                }
            }
        }

        mod given_fifty_fifty_chance {
            mod and_zero_coefficient {
                #[test]
                fn does_not_change_the_original_chromosome() {
                    todo!();
                }
            }

            mod and_nonzero_coefficient {
                #[test]
                fn slightly_changes_the_original_chromosome() {
                    todo!();
                }
            }
        }

        mod given_max_chance {
            mod and_zero_coefficient {
                #[test]
                fn does_not_change_the_original_chromosome() {
                    todo!();
                }
            }

            mod and_nonzero_coefficient {
                #[test]
                fn entirely_changes_the_original_chromosome() {
                    todo!();
                }
            }
        }
    }
}

Naming tests this way took me a while to get used to, but eventually I've found this convention so helpful that I cannot not mention it; tests structured like that are worth more than a million comments, because tests - contrary to comments - don't become obsolete over time.

When implementing, to avoid copy-pasting, let's create a helper function:

#[cfg(test)]
mod tests {
    /* ... */

    mod gaussian_mutation {
        use super::*;

        fn actual(chance: f32, coeff: f32) -> Vec<f32> {
            let mut rng = ChaCha8Rng::from_seed(Default::default());
            let mut child = vec![1.0, 2.0, 3.0, 4.0, 5.0].into_iter().collect();

            GaussianMutation::new(chance, coeff).mutate(&mut rng, &mut child);

            child.into_iter().collect()
        }

        /* ... */
    }
}

... and with it, the rest is as easy as:

# ...

[dev-dependencies]
approx = "0.4"
rand_chacha = "0.3"

#[cfg(test)]
mod tests {
    /* ... */

    mod gaussian_mutation {
        /* ... */

        mod given_zero_chance {
            use approx::assert_relative_eq;

            fn actual(coeff: f32) -> Vec<f32> {
                super::actual(0.0, coeff)
            }

            mod and_zero_coefficient {
                use super::*;

                #[test]
                fn does_not_change_the_original_chromosome() {
                    let actual = actual(0.0);
                    let expected = vec![1.0, 2.0, 3.0, 4.0, 5.0];

                    assert_relative_eq!(actual.as_slice(), expected.as_slice());
                }
            }

            mod and_nonzero_coefficient {
                use super::*;

                #[test]
                fn does_not_change_the_original_chromosome() {
                    let actual = actual(0.5);
                    let expected = vec![1.0, 2.0, 3.0, 4.0, 5.0];

                    assert_relative_eq!(actual.as_slice(), expected.as_slice());
                }
            }
        }

        /* ... */
    }
}

Implementing rest of the tests follows what we've learned so far, so it's been - brace for it - left as an exercise for the reader :-)

Now we can pass MutationMethod next to SelectionMethod - there are no generics inside MutationMethod::mutate(), so let's not hesitate on a Box:

pub struct GeneticAlgorithm<S> {
    selection_method: S,
    crossover_method: Box<dyn CrossoverMethod>,
    mutation_method: Box<dyn MutationMethod>,
}

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    pub fn new(
        selection_method: S,
        crossover_method: impl CrossoverMethod + 'static,
        mutation_method: impl MutationMethod + 'static,
    ) -> Self {
        Self {
            selection_method,
            crossover_method: Box::new(crossover_method),
            mutation_method: Box::new(mutation_method),
        }
    }

    /* ... */
}

... and then:

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    /* ... */

    pub fn evolve<I>(/* ... */) -> Vec<I>
    where
        I: Individual,
    {
        /* ... */

        (0..population.len())
            .map(|_| {
                /* ... */

                self.mutation_method.mutate(rng, &mut child);

                /* ... */
            })
            .collect()
    }
}

Coding: Creating individuals

Our child is of type Chromosome, while the vector we return is Vec<I> - so the last thing we're missing is the ability of converting a genotype back into an individual:

pub trait Individual {
    fn create(chromosome: Chromosome) -> Self;

    /* ... */
}

/* ... */

#[cfg(test)]
mod tests {
    /* ... */

    impl Individual for TestIndividual {
        fn create(chromosome: Chromosome) -> Self {
           todo!()
        }

        /* ... */
    }
}

... and then voilà!

impl<S> GeneticAlgorithm<S>
where
    S: SelectionMethod,
{
    /* ... */

    pub fn evolve<I>(&self, rng: &mut dyn RngCore, population: &[I]) -> Vec<I>
    where
        I: Individual,
    {
        assert!(!population.is_empty());

        (0..population.len())
            .map(|_| {
                let parent_a = self.selection_method.select(rng, population).chromosome();
                let parent_b = self.selection_method.select(rng, population).chromosome();
                let mut child = self.crossover_method.crossover(rng, parent_a, parent_b);

                self.mutation_method.mutate(rng, &mut child);

                I::create(child)
            })
            .collect()
    }
}

The Test

Having .evolve() ready, the time has come for perhaps the most exciting slice of this post: the test that'll prove to everyone that our .evolve() works and that we know what we're doing.

We'll start by adjusting our TestIndividual so that instead of panic!()-ing, it actually implements ::create() and .chromosome().

Some tests - e.g. the ones for RouletteWheelSelection - don't care about genes at all, so we'll get bonus points for inventing a solution that doesn't require modifying those already-working tests.

My proposition is to change TestIndividual from struct to an enum with two different variants:

#[cfg(test)]
mod tests {
    /* ... */

    #[derive(Clone, Debug)]
    enum TestIndividual {
        /// For tests that require access to the chromosome
        WithChromosome { chromosome: Chromosome },

        /// For tests that don't require access to the chromosome
        WithFitness { fitness: f32 },
    }

    impl TestIndividual {
        fn new(fitness: f32) -> Self {
            Self::WithFitness { fitness }
        }
    }

    impl Individual for TestIndividual {
        fn create(chromosome: Chromosome) -> Self {
            Self::WithChromosome { chromosome }
        }

        fn chromosome(&self) -> &Chromosome {
            match self {
                Self::WithChromosome { chromosome } => chromosome,

                Self::WithFitness { .. } => {
                    panic!("not supported for TestIndividual::WithFitness")
                }
            }
        }

        fn fitness(&self) -> f32 {
            match self {
                Self::WithChromosome { chromosome } => {
                    chromosome.iter().sum()

                    // ^ the simplest fitness function ever - we're just
                    // summing all the genes together
                }

                Self::WithFitness { fitness } => *fitness,
            }
        }
    }

    /* ... */
}

(instead of enum, you could also create two separate types like TestIndividualWithChromosome and TestIndividualWithFitness, but that feels too enterprisey for me)

Since we're already here, let's derive PartialEq - it'll come handy in a moment:

#[cfg(test)]
mod tests {
    /* ... */

    #[derive(Clone, Debug, PartialEq)]
    pub enum TestIndividual {
        /* ... */
    }

    /* ... */

    impl PartialEq for Chromosome {
        fn eq(&self, other: &Self) -> bool {
            approx::relative_eq!(self.genes.as_slice(), other.genes.as_slice())
        }
    }

    /* ... */
}

As for the test, nothing scary - we'll start with a few individuals, evolve them over a couple of generations and see how they end up looking like:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn genetic_algorithm() {
        let mut rng = ChaCha8Rng::from_seed(Default::default());

        let ga = GeneticAlgorithm::new(
            RouletteWheelSelection,
            UniformCrossover,
            GaussianMutation::new(0.5, 0.5),
        );

        let mut population = vec![
            /* TODO */
        ];

        // We're running `.evolve()` a few times, so that the differences between the
        // input and output population are easier to spot.
        //
        // No particular reason for a number of 10 - this test would be fine for 5, 20 or
        // even 1000 generations - the only thing that'd change is the magnitude of the
        // difference between the populations.
        for _ in 0..10 {
            population = ga.evolve(&mut rng, &population);
        }

        let expected_population = vec![
            /* TODO */
        ];

        assert_eq!(population, expected_population);
    }

    /* ... */
}

We're going to create a few individuals at once, so a helper function is a must:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn genetic_algorithm() {
        fn individual(genes: &[f32]) -> TestIndividual {
            TestIndividual::create(genes.iter().cloned().collect())
        }

        /* ... */
    }

    /* ... */
}

... and now:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn genetic_algorithm() {
        /* ... */

        let mut population = vec![
            individual(&[0.0, 0.0, 0.0]),
            individual(&[1.0, 1.0, 1.0]),
            individual(&[1.0, 2.0, 1.0]),
            individual(&[1.0, 2.0, 4.0]),
        ];

        /* ... */

        let expected_population = vec![
            individual(&[0.0, 0.0, 0.0, 0.0]),
            individual(&[0.0, 0.0, 0.0, 0.0]),
            individual(&[0.0, 0.0, 0.0, 0.0]),
            individual(&[0.0, 0.0, 0.0, 0.0]),
        ];

        /* ... */
    }
}

(as before, there's no reason for having exactly 4 individuals with exactly 3 genes - it just feels reasonable to maintain; two individuals would be too few, a hundredth - probably too many.)

Do you hear the people sing, singings the songs of angry men? It's cargo test, failing due to the zeroed-out expected_population:

thread '...' panicked at 'assertion failed: `(left == right)`
  left: `[WithChromosome { ... }, WithChromosome { ... }, ... ]`,
 right: `[WithChromosome { ... }, WithChromosome { ... }, ... ]`,

Using this output, we can copy-paste actual genes from left into expected_population:

#[cfg(test)]
mod tests {
    /* ... */

    #[test]
    fn genetic_algorithm() {
        /* ... */

        let expected_population = vec![
            individual(&[0.44769490, 2.0648358, 4.3058133]),
            individual(&[1.21268670, 1.5538777, 2.8869110]),
            individual(&[1.06176780, 2.2657390, 4.4287640]),
            individual(&[0.95909685, 2.4618788, 4.0247330]),
        ];

        /* ... */
    }
}

Yes...​ ha ha ha...​ yes... we've got...​ numbers?

What's certain is that we've got some output - but how do we know those four individuals are actually better than the four individuals we'v started with?

Well, we can compare their fitness scores!

// In this case, `fitness score` means `average of the genes`, as per our implemetation
// inside `TestIndividual::fitness()`

let population = vec![
    individual(&[/* ... */]), // fitness = 0.0
    individual(&[/* ... */]), // fitness = 1.0
    individual(&[/* ... */]), // fitness ~= 1.33
    individual(&[/* ... */]), // fitness ~= 2.33
];

let expected_population = vec![
    individual(&[/* ... */]), // fitness ~= 6.8
    individual(&[/* ... */]), // fitness ~= 5.7
    individual(&[/* ... */]), // fitness ~= 7.8
    individual(&[/* ... */]), // fitness ~= 7.4
];

it works! it works! our genetic algorithm is the apex predator of computer science!

We've got higher fitness scores, which means that our individuals got better and everything worked as intended:

1. Thanks to the roulette wheel selection, the worst solution - [0.0, 0.0, 0.0] - was discarded.

2. Thanks to the uniform crossover, the average fitness score grew from 3.5 to 7.0 (!)

3. Thanks to the Gaussian mutation, we see genes - numbers - that were not present in the initial population.

You don't have to believe me, though - try commenting out various parts of the algorithm:

// self.mutation_method.mutate(rng, &mut child);

... and see how they affect the output population.

Closing thoughts

So far, learning whoa so much on the way, we've implemented two separate components: a neural network and a genetic algorithm.

In the upcoming, last post of this series we'll integrate both algorithms and implement a snazzy user interface that'll allow us to see beyond lists of floating-point numbers - as promised, that's where the JavaScript and WebAssembly will come to play.